Fibonacci 的相关规律题及计算

hello kity

期待您的批阅，由于写解题报告时不一定考虑的很周到，所以如果您有什么不懂的地方，请您留言，然而一天之内我肯定会看见您信息，再对代码注释详细，让您更好的阅读

分类

HDU （1893 Sibonacci Numbers）

题目大意：

f(1)=1
f(2)=1
f(n)=f(n-1)+f(n-2) (n>=3)

Now Sempr found another Numbers, he named it "Sibonacci Numbers", the definition is below:
f(x)=0 (x<0)
f(x)=1 (0<=x<1)
f(x)=f(x-1)+f(x-3.14) (x>=1)

题目分析：

这个题目是黑书上的弱化版，黑书有对这一系列问题进行讨论，然后这里，你只需要把数放大100倍，这样只要递归求解就可以了，注意要用字符串里出来输入的数据哦，因为我们最多只需要小数点后的2位，后面都舍去‘

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long s[100100];
int init(){
    int i;
    for(i=0;i<=100;i++)
        s[i]=1;
    for(i=100;i<=100100;i++){
        if(i<314)
            s[i]=s[i-100]%1000000007;
        else
            s[i]=(s[i-100]+s[i-314])%1000000007;
    }
    return 0;
}
int main(){
    int cas,n,i;
    char ch[20];
    init();
    scanf("%d",&cas);
    while(cas--){
        scanf("%s",ch);
        if(ch[0]=='-'){
            printf("0\n");
            continue;    
        }
        i=0;
        n=0;
        int len=strlen(ch);
        while(ch[i]!='.'&&i<len)
            n=n*10+ch[i++]-'0';
        if(i+1<len)
            n=n*10+ch[i+1]-'0';
        else
            n=n*10;
        if(i+2<len)
            n=n*10+ch[i+2]-'0';
        else
            n=n*10;
        printf("%lld\n",s[n]);
    }
    return 0;
}

HDU （超级楼梯）

题目大意：

有一楼梯共M级，刚开始时你在第一级，若每次只能跨上一级或二级，要走上第M级，共有多少种走法？

题目分析：
画个图也许您就明白了，如果您再加上一个台阶，图中就会多出两条线，一个是从n-2那里引来的，一条是从n-1那里引来的，所以F[N]=F[N-1]+F[N-2]
想必猜出来了这是什么了吧呵呵
这就是典型的feibonacci数
公式：
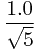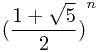f[n]= $\frac{1.0}{\sqrt{5}}$ { ${(\frac{1+\sqrt{5}}{2})}^{n}$ - ${(\frac{1-\sqrt{5}}{2})}^{n}$ }
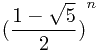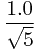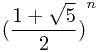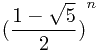但是这里直接模拟求解就可以了
代码：

#include<iostream>
#include<cstdio>
using namespace std;
long long s[45];
int main(){
    int i,n,cas;
    s[1]=1;
    s[2]=1;
    for(i=3;i<=40;i++)
        s[i]=s[i-1]+s[i-2];
    cin>>cas;
    while(cas--){
        scanf("%d",&n);
        printf("%lld\n",s[n]);
    }
    return 0;
}