致我们的程序路
算法这条路,真的很漫长,让我们大家都受益匪浅。我们计算机专业虽然不是每个方向都需求算法,但是思想肯定应用到各个领域的每个角落。近期忙着各种事情,学习各种新东西,我想人的一生中就是这样不断学习,接触新东西的过程吧。。。 在此我对广大给我留言的朋友说声抱歉,因为没能及时回复大家的问题。 我想以后我会改的了, 要拿出一些时间出来跟大家分享知识, 向大家学习。 最近在学 UNIX 网络编程, 所以我在这里重新还开个模块,记录UNIX网络编程的点点滴滴,当然算法我还是不会放弃的,要不断温故 学习,总结。 2013年, 你准备好了吗? 如果有比较好的算法,请联系我,我帮大家总结 刊登出来放在上面供广大同学学习。
HDU (1895 Sum Zero 比较技巧型的模拟+hash)
题目大意:给你5组数,让你求A[0][i]+A[1][j]+A[2][k]+A[3][l]+A[4][m]=0的组数
题目分析:如果直接暴力枚举的话,唉,肯定超时,5重循环想都不用想了,我们看看这题的思路吧,我也是参考大牛的思路的,这里的优化很高效,大家注意分析哦{^_^};首先我们把5行中的4行 两两进行相加合成二行,然后我们这里只有3组数据,然后对数据进行稍微处理一下,首先把其中的两行进行排序,头两行进行从大到小的排序,最后一行从小到大排序,然后我们遍历第一行,作为外循环,然后从第二行的第一个开始(每次遍历都从第二行的第一个开始的),把tempt下标停到第三行足够大的位置上,也就是满足前面两个加上该位置的值大于等于0,因为前面两行数据都是递减排列的,前面不满足后面肯定不满足,所以下次讨论的时候只需要从tempt位置开始讨论,这样节约了很多不必要的时间。以后的讨论都从上次的tempt的位置开始,因为前面与第三个加起来小于0,我遍历下去的值肯定也是小于0,所以只需要从tempt开始。
代码+部分注释:
#include<iostream>
#include<cstdio>
#include<algorithm>
#define N 302
using namespace std;
int B[N*N],s[3][N*N],A[5][N*N],cnt[5][N*N],num[5];
int get(int n,int k,int C[]){
int i,j;
for(i=0;i<=n;i++)
cnt[k][i]=0;
j=0;
s[k][0]=C[0];
cnt[k][0]=1;
for(i=1;i<n;i++){
if(s[k][j]!=C[i])
s[k][++j]=C[i];
cnt[k][j]++;//这个是记录各个情况的次数的
}
num[k]=j+1;
return 0;
}
int cmp(int a,int b){
return a>b;
}
int main(){
int cas,n,i,j,tempt,pos,ans,k;
int xx;
scanf("%d",&cas);
while(cas--){
ans=0;
for(j=0;j<=4;j++){
scanf("%d",&n);
num[j]=n;
for(i=0;i<n;i++)
scanf("%d",&A[j][i]);
}
sort(A[0],A[0]+num[0],cmp);
get(num[0],0,A[0]);
k=0;
for(i=0;i<num[1];i++)
for(j=0;j<num[2];j++)
B[k++]=A[1][i]+A[2][j];
num[1]=k;
sort(B,B+num[1],cmp);
//注意第三行是从小到大哦!
get(num[1],1,B);
k=0;
for(i=0;i<num[3];i++)
for(j=0;j<num[4];j++)
B[k++]=A[3][i]+A[4][j];
num[3]=k;
sort(B,B+num[3]);
get(num[3],2,B);
tempt=0;
for(i=0;i<num[0];i++){
xx=s[0][i]+s[1][0];
while(tempt<num[2]&&xx+s[2][tempt]<0)
tempt++;
if(tempt==num[2])
//这里说明没有任何一种情况的和是大于等于0的
//所以没必要讨论了 还是那句话,因为前两行
//是从大到小排列的,前面的情况的和小于0后
//面就不用考虑了
break;
if(xx+s[2][tempt]==0)
ans+=cnt[0][i]*cnt[1][0]*cnt[2][tempt];
pos=tempt;
for(j=1;j<num[1];j++){
xx=s[0][i]+s[1][j];
while(pos<num[2]&&xx+s[2][pos]<0)
pos++;
if(pos==num[2])
break;
if(xx+s[2][pos]==0)
ans+=cnt[0][i]*cnt[1][j]*cnt[2][pos];
}
}
printf("%d\n",ans);
}
return 0;
}
POJ (2739 Sum of Consecutive Prime Numbers)
题目分析:直接枚举就可以了 二重循环!
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int pri[10000],k;
bool flag[10001];
int get_pri(){
int i;
memset(flag,true,sizeof(flag));
pri[1]=2;
k=1;
for(i=4;i<=10000;i+=2)
flag[i]=false;
for(i=3;i<=10000;i+=2)
if(flag[i]){
pri[++k]=i;
for(int j=i*2;j<=10000;j+=i)
flag[j]=false;
}
return 0;
}
int main(){
int i,j;
int n,ans,sum;
get_pri();
while(scanf("%d",&n),n){
ans=0;
int x=n/2;
for(i=1;pri[i]<=x;i++){
sum=0;
for(j=i;j<=x;j++){
sum+=pri[j];
if(sum==n){
ans++;
break;
}
if(sum>n)
break;
}
}
if(flag[n])
ans++;
printf("%d\n",ans);
}
return 0;
}
HDU 1568(非常经典微妙的 斐波纳契计算)
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来,CodeStar决定要考考他,于是每问他一个数字,他就要把答案说出来,不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了,可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。
0 1 2 3 4 5 35 36 37 38 39 40
0 1 1 2 3 5 9227 1493 2415 3908 6324 1023
题目分析:这个题目非常精美!首先题目要求求第N个斐波纳契数的前四位,前提是他不止四位哦!
然后引用到的知识点,斐波纳契的计算公式: (1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)
(1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)
还有对数log()的作用,先让我们回忆一下log 的运算性质吧~
1)log(a*b)=log(a)+log(b); 2)log(a/b)=log(a)-log(b);
其实在数学里面,log可以求一个大数的科学计数法的数值部分,比如说123456
首先log10(1234567)=log(1.234567*10^6)=log(1.234567)+6; 然后log10(1.234567)就是log10(1234567)的小数位
然后10^log10(1.234567)=1.234567,所以通过这样的转换 我们可以很巧妙的得到了一个很大的数的科学计数法的表示值!
然后您要取4位就拿4位!要多少位就拿多少位!
既然这样可以我们就干下去吧!
斐波纳契的计算公式: (1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)
(1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)
log10( (1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n])
(1/√5) * [((1+√5)/2)^n-((1-√5)/2)^n])
化简一下得到:
-0.5*log10(5.0)+((double)n)*log(f)/log(10.0)+log10(1-((1-√5)/(1+√5))^n)其中f=(sqrt(5.0)+1.0)/2.0;
在这里 log10(1-((1-√5)/(1+√5))^n)无穷小可以忽略不计!
最后得到 log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0) !
然后就是直接贴代码了
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int s[21]={0,1,1,2};
const double f=((double)sqrt(5)+1)/2.0;
void get_Fibonacci(int x){
if(x<=20)
printf("%d\n",s[x]);
else{
double ans=(-0.5)*log(5.0)/log(10.0)+(double(x))*log(f)/log(10.0);
ans=ans-floor(ans);
double k=pow(10.0,ans);
//cout<<"k= "<<k<<endl;
while(k<1000.0)
k*=10.0;
printf("%d\n",(int)k);
}
}
int main(){
int x,i;
for(i=3;i<=20;i++)
s[i]=s[i-1]+s[i-2];
//在这里为了区别其他多于4位的答案我先把4位以内的
//都计算好存起来!
while(~scanf("%d",&x)){
if(x==0){
printf("0\n");
continue;
}
get_Fibonacci(x);
}
return 0;
}
HDU 1717(小数化分数2 --非常犀利)
题目大意:
|
Problem Description
Ray 在数学课上听老师说,任何小数都能表示成分数的形式,他开始了化了起来,很快他就完成了,但他又想到一个问题,如何把一个循环小数化成分数呢?
请你写一个程序不但可以将普通小数化成最简分数,也可以把循环小数化成最简分数。 |
|
Input
第一行是一个整数N,表示有多少组数据。
每组数据只有一个纯小数,也就是整数部分为0。小数的位数不超过9位,循环部分用()括起来。 |
|
Output
对每一个对应的小数化成最简分数后输出,占一行。
|
|
Sample Input
3 0.(4) 0.5 0.32(692307) |
|
Sample Output
4/9 1/2 17/52 |
题目大意分析:这个思路非常精妙,刚开始的时候我推到一半,差点就出来了,但是还是没自信以为这样是错的,后来看完各位神牛的思路,果断肯定了 。这个题目的解题思路非常值得学习!
首先跟你一个小数 令X= 0 . s1 s2 ..sn ( y1 y2 y3..ym ) 这样的话我们把小数点分为三个部分,分别用三种颜色标记了!
我们可以把表达式转换成:X * 10 ^n=s1s2..sn+0.y1y2..ym; 我们用S1替换 s1s2..sn ,Y替换 0.(y1y2..yn), 然后可以把表达式写成: X * 10^n=S1 + Y; 然后 Y=0.(y1y2..ym) 变形一下:Y * 10 ^m=y1y2..ym + Y; 在这里我们另y1y2..ym等于S2;
宗上所述:我们得到两个表达式 X * 10^n=S1 + Y; Y * 10^m=S2 + Y; 然后将两个式子合并成一个用表达式,
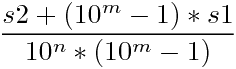 然后就可以根据这个公式,求出分子分母的 最大公约式 然后化简 就可以了{^_^}
然后就可以根据这个公式,求出分子分母的 最大公约式 然后化简 就可以了{^_^}
代码如下:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int gcd(int x,int y){
int c;
if(x<y){
c=y; y=x;
x=c;
}
if(y==0)
return x;
return gcd(y,x%y);
}
int main(){
char ch[25];
int cas,i,p1,k1,p2,k2;
int t1,t2,len;
scanf("%d",&cas);
while(cas--){
scanf("%s",ch);
len=strlen(ch);
//cout<<"len = "<<len<<endl;
i=0;
while(ch[i]!='.')
i++;
p1=0; k1=1;
while((ch[++i]!='(')&&(i<len)){
p1=p1*10+ch[i]-'0';
k1*=10;
}
//cout<<"p1 = "<<p1<<"k1 = "<<k1<<endl;
p2=0; k2=1;
while(ch[++i]!=')'&&i<len){
p2=p2*10+ch[i]-'0';
k2*=10;
}
//cout<<"p2 = "<<p2<<"k2 = "<<k2<<endl;
if(p2){
t1=p1*(k2-1)+p2;
t2=(k2-1)*k1;
}
else{
t1=p1;
t2=k1;
}
int w=gcd(t1,t2);
printf("%d/%d\n",t1/w,t2/w);
}
return 0;
}
HDU 1271(整数对 经典!)
题目大意:
所以现在小希希望你编写一个程序,来帮助她找到尽可能多的解。
例如,Gardon想的是A=31,B=3 告诉小希N=34,
小希除了回答31以外还可以回答27(27+7=34)所以小希可以因此而得到一个额外的糖果。
对于每个输入的N,输出所有符合要求的解(按照大小顺序排列)如果没有这样的解,输出"No solution."
题目分析:第一次,我的思路是从一半开始枚举,发现这样超时了
TLE代码:
#include<iostream>
#include<stdio.h>
#include<math.h>
using namespace std;
int s[1000];
inline int solve(int x){
int k,ans,i,j;
int c,sum,t,times=1;
while(c){
c/=10;
k++;
}
int xx=pow(10,k-2);
for(i=xx;i<=x;i++){
k=0; c=i;
while(c){
c/=10;
k++;
}
for(j=1;j<=k;j++){
c=i;
sum=0;
int w=(int)pow(10,k-j);
if(j==1){
sum=c%w;
}
if(j==k){
sum=c/10;
}
if(j!=k&&j!=1){
t=c%w;
int p=c/w;
p/=10;
p=p*((int)pow(10,k-j));
sum=p+t;
}
if(sum+i==x){
s[times++]=i;
}
}
}
return times-1;
}
int main(){
int x,t,i;
while(scanf("%d",&x),x){
t=solve(x);
if(t==0)
printf("No solution.\n");
else{
for(i=1;i<=t;i++)
printf("%d ",s[i]);
printf("\n");
}
}
return 0;
}
后来看了一下解题报告,后来终于理解了,现在让我来说说这题的做法跟规律吧{^_^}
首先假设X的第k位拿走,然后加上加上X的和正好等于N!
这样的话 我们可以把X 分解成:X= a+b * 10^k +c * 10^( k+1 ); 这里特别强调一下, a代表的是比第k位后面的低位数子,可能是多位,b仅仅代表一个数值,即你选择拿开的那位数,c代表的是比k位高的高位数字,例如:12345 您想拿走3的话 这时候a=45,c=12,b=3; 然后拿走之后就会组合成另一个数:Y=a + c * 10^k; 然后X+Y=2 * a + b * 10 ^k +11 * c * 10^k;
现在如果N=X+Y;他必定满足上面那种结构!所以我们考虑这种结构特征就可以了,首先上述表达式的低位是2*a 可能发生进位!
所以b的值可能是10,但是 都不影响c的值, 这个时候只需要分两种不同的b的情况,来求出a,然后验证一下 是不是等于N就可以了!
AC代码如下:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<set>
using namespace std;
void solve(int x,set<int> &result){
int k,high,b2,a;
int c,sum,b1;
for(k=1;k<=x;k*=10){
high=x/k;
c=high/11;
c*=k;
b1=high%11;
if((b1!=0||c!=0)&&b1<10){
b1*=k;
a=(x-b1-11*c)/2;
if(2*a+b1+11*c==x)
result.insert(a+b1+c*10);
}
b2=high%11-1;
if((b2!=0||c!=0)&&b2>=0){
b2*=k;
int a2=(x-b2-11*c)/2;
if(x==2*a2+b2+11*c)
result.insert(a2+b2+10*c);
}
}
}
int main(){
int x,i;
while(cin>>x,x){
set<int>result;
//set结构不仅可以排序,而且可以去除重复的
//下次要多多学习,总结!
solve(x,result);
if(result.empty()){
printf("No solution.\n");
}
else{
set<int>::iterator it=result.begin();
printf("%d",*it);
while(++it!=result.end())
printf(" %d",*it);
printf("\n");
}
}
return 0;
}
还有一种代码思路一样
AC代码
#include<iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
int s[1000],times;
int cmp(int x,int y){
return x<y;
}
int solve(int x){
int k,high,b2,a;
int c,sum,b1;
times=0;
for(k=1;k<=x;k*=10){
high=x/k;
c=high/11;
c*=k;
b1=high%11;
if((b1!=0||c!=0)&&b1<10){
b1*=k;
a=(x-b1-11*c)/2;
if(2*a+b1+11*c==x)
s[++times]=a+b1+c*10;
}
b2=high%11-1;
if((b2!=0||c!=0)&&b2>=0){
b2*=k;
a=(x-b2-11*c)/2;
if(x==2*a+b2+11*c)
s[++times]=a+b2+10*c;
}
}
return 0;
}
int main(){
int x,t,i;
while(scanf("%d",&x)&&x){
solve(x);
if(times==0){
printf("No solution.\n");
}
else{
sort(s+1,s+1+times,cmp);
printf("%d",s[1]);
for(i=2;i<=times;i++){
if(s[i]!=s[i-1])
printf(" %d",s[i]);
}
printf("\n");
}
}
return 0;
}
题目总结:今后一定要大量深入学校STL函数!还有这题的去除重复不能忘记,同时要深刻认识本题的思路,太巧妙,强大了
HDU 1215(七夕节)
题目大意:您的编号N的因子和就是您的另一半的编号!数字N的因子就是所有比N小又能被N整除的所有正整数,如12的因子有1,2,3,4,6.输入数据的第一行是一个数字T(1<=T<=500000),它表明测试数据的组数.然后是T组测试数据,每组测试数据只有一个数字N(1<=N<=500000).
题目分析:其实是水题!一开始想复杂了,后来想想看,我们只要找i :1->sqrt(N)然后用通过N/i 找到比sqrt(N)大的满足要求的因子!
这样最坏情况下也才500000*3000最多!还是不会超时的
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int solve(int x){
int i,j,sum=0;
double tempt=sqrt(x);
for(i=2;i<=tempt;i++){
if(x%i==0){
sum+=i;
int t=x/i;
if(t!=i){
sum+=t;
//是在里面判断比sqrt(N)大的因子合法与否!
}
}
}
sum+=1;
return sum;
}
int main(){
int cas,t,ans;
scanf("%d",&cas);
while(cas--){
scanf("%d",&t);
ans=solve(t);
printf("%d\n",ans);
}
return 0;
}
HDU 2504(又见GCD)
题目:
有三个正整数a,b,c(0<a,b,c<10^6),其中c不等于b。若a和c的最大公约数为b,现已知a和b,求满足条件的最小的c。
刚刚开始的时候写错了,没考虑太多,直接a/b如果不等于1 就a/b-1然后乘以b!
其实枚举就行了:
#include<iostream>
#include<cstdio>
using namespace std;
int gcd(int x,int y){
int c;
if(x<y){
c=y;
y=x%y;
x=c;
}
while(y){
c=y;
y=x%y;
x=c;
}
return x;
}
int main(){
int a,b,c,flag,cas;
cin>>cas;
while(cas--){
scanf("%d %d",&a,&b);
for(int i=2;;i++){
if(gcd(a,i*b)==b){
flag=i;
break;
}
}
printf("%d\n",flag*b);
}
return 0;
}
总结:唉,汗颜!下次细心!UP!
HDU 1722(分蛋糕 规律性题目)
一次生日Party可能有p人或者q人参加,现准备有一个大蛋糕.问最少要将蛋糕切成多少块(每块大小不一定相等),才能使p人或者q人出席的任何一种情况,都能平均将蛋糕分食.
题目分析:p+q-gcd(p+q)
代码:
#include<iostream>
#include<cstdio>
using namespace std;
int gcd(int a,int b){
int c;
if(a<b){
c=a; a=b;
b=c;
}
while(b){
c=b;
b=a%b;
a=c;
}
return a;
}
int main(){
int x,y;
while(~scanf("%d %d",&x,&y)){
printf("%d\n",x+y-gcd(x,y));
}
return 0;
}
猴子分桃(很有趣的规律题)
题目大意:老猴子辛苦了一辈子,给那群小猴子们留下了一笔巨大的财富——一大堆桃子。
老猴子决定把这些桃子分给小猴子。
第一个猴子来了,它把桃子分成五堆,五堆一样多,但还多出一个。它把剩下的一个留给老猴子,自己拿走其中的一堆。
第二个猴子来了,它把桃子分成五堆,五堆一样多,但又多出一个。它把多出的一个留给老猴子,自己拿走其中的一堆。
后来的小猴子都如此照办。最后剩下的桃子全部留给老猴子。
这里有n只小猴子,请你写个程序计算一下在开始时至少有多少个桃子,以及最后老猴子最少能得到几个桃子。
题目分析:其实题目不是很难,但是我很悲剧的是,因为学校服务器的问题,害我WA了20多次,后来都别的网站上提交,1Y就过了!
这里表示非常不淡定。。。
废话不说了让我们看题目吧:假设有X个桃子,第一次把X个桃子分成5份,恰好多了1,然后拿走一份!再这里,您应该想到借他4个不就正好5份了麽?然后每次都不是5份了麽?最后当前猴子拿走的也没多拿不是麽?举个例子说明一下吧,假设有5只猴子,第一次每份
(X-1)/5;如果我们借给他4个,每份不就是(X+4)/5吗?然后您会发现,(X+1)/5=(X-1)/5+1;每次都是如此,然后每次都能被5整除,这很显然,所以您应该懂了吧~{^_^}X=5^n-4 老猴子得到=n+(X+4)*(4/5)^n-4(您得还我的呀!对吧 嘿嘿)
代码+部分注释:
#include<iostream>
#include<cstdio>
#include<math.h>
using namespace std;
int main(){
long long total_num,old_num;
int n;
while(cin>>n,n){
total_num=pow(5,n)-4;
old_num = n + (total_num+4)*(pow(0.8,n))-4;
cout<<total_num<<" "<<old_num<<endl;
}
return 0;
}