HDU 1717（小数化分数2 --非常犀利）

spoiler posted @ 2011年4月18日 00:12 in 未分类 , 2415 阅读

题目大意：

Problem Description

Ray 在数学课上听老师说，任何小数都能表示成分数的形式，他开始了化了起来，很快他就完成了，但他又想到一个问题，如何把一个循环小数化成分数呢?
请你写一个程序不但可以将普通小数化成最简分数，也可以把循环小数化成最简分数。

Input

第一行是一个整数N，表示有多少组数据。
每组数据只有一个纯小数，也就是整数部分为0。小数的位数不超过9位，循环部分用()括起来。

Output

对每一个对应的小数化成最简分数后输出，占一行。

Sample Input

3
0.(4)
0.5
0.32(692307)

Sample Output

4/9
1/2
17/52

题目大意分析：这个思路非常精妙，刚开始的时候我推到一半，差点就出来了，但是还是没自信以为这样是错的，后来看完各位神牛的思路，果断肯定了。这个题目的解题思路非常值得学习！

首先跟你一个小数令X= 0 . s1 s2 ..sn ( y1 y2 y3..ym ) 这样的话我们把小数点分为三个部分，分别用三种颜色标记了！

我们可以把表达式转换成：X * 10 ^n=s1s2..sn+0.y1y2..ym; 我们用S1替换 s1s2..sn ，Y替换 0.（y1y2..yn）, 然后可以把表达式写成： X * 10^n=S1 + Y; 然后 Y=0.（y1y2..ym）变形一下：Y * 10 ^m=y1y2..ym + Y; 在这里我们另y1y2..ym等于S2；

宗上所述：我们得到两个表达式 X * 10^n=S1 + Y； Y * 10^m=S2 + Y; 然后将两个式子合并成一个用表达式，

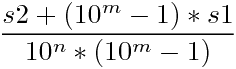$\frac{s2 + (10^m-1)*s1}{10^n * ( 10^m -1 )}$ 然后就可以根据这个公式，求出分子分母的最大公约式然后化简就可以了{^_^}

代码如下：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int gcd(int x,int y){
	int c;
	if(x<y){
		c=y;	y=x;
		x=c;
	}
	if(y==0)
		return x;
	return gcd(y,x%y);
}
int main(){
	char ch[25];
	int cas,i,p1,k1,p2,k2;
	int t1,t2,len;
	scanf("%d",&cas);
	while(cas--){
		scanf("%s",ch);
		len=strlen(ch);
		//cout<<"len = "<<len<<endl;
		i=0;	
		while(ch[i]!='.')
			i++;
		p1=0;	k1=1;
		while((ch[++i]!='(')&&(i<len)){
			p1=p1*10+ch[i]-'0';
			k1*=10;
		}
		//cout<<"p1 = "<<p1<<"k1 = "<<k1<<endl;
		p2=0;	k2=1;
		while(ch[++i]!=')'&&i<len){
			p2=p2*10+ch[i]-'0';
			k2*=10;
		}
		//cout<<"p2 = "<<p2<<"k2 = "<<k2<<endl;
		if(p2){
			t1=p1*(k2-1)+p2;
			t2=(k2-1)*k1;
		}
		else{
			t1=p1;
			t2=k1;
		}
		int w=gcd(t1,t2);
		printf("%d/%d\n",t1/w,t2/w);
	}
	return 0;
}