ZOJ (3497 Mistwald 关于矩阵求点直接连通的问题)
题目大意:给你一个N*M 的矩阵, 矩阵里的每个点代表一个全送阵, 代表当前点可以全送到4个点,你的出发点是(1,1);要到达的点是(n,m),这里要注意的是,一旦任何点到了(n,m)点之后 就会被全送出去,离开整个地图,所以这里算是一个陷阱,您要把(n,m)点能够到达的点,全部置0,(”0“代表他不能到达某个点)
题目分析:
这里是Maxtrix67 大牛总结的 第八个矩阵的经典应用:
给定一个有向图,问从A点恰好走k步(允许重复经过边)到达B点的方案数mod p的值
把 给定的图转为邻接矩阵,即A(i,j)=1当且仅当存在一条边i->j。令C=A*A,那么C(i,j)=ΣA(i,k)*A(k,j),实际上就 等于从点i到点j恰好经过2条边的路径数(枚举k为中转点)。类似地,C*A的第i行第j列就表示从i到j经过3条边的路径数。同理,如果要求经过k步的 路径数,我们只需要二分求出A^k即可;
题目让我们求的是他们是否连通,这里只需用1与0带入即可,
我们这里在乘的过程不是求和,而是用到“与”操作,因为我们要得出的结果不是路径数,而是 是否能经过K步到达该点~
代码+部分注释:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M {
int s[30][30];
};
struct M unit;
int n;
struct M multiply(struct M a,struct M b){
struct M c;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
c.s[i][j]=0;
for(int k=1;k<=n;k++)
//:注意下面这个操作,是“|”而不是“+”这里是求是否能到达
//而不是求 到达的路径数目!
c.s[i][j]=(c.s[i][j]|a.s[i][k]*b.s[k][j]);
}
return c;
}
struct M paw(struct M a,int t){
struct M ans=unit;
struct M b=a;
while(t){
if(t%2==1)
ans=multiply(ans,b);
b=multiply(b,b);
t/=2;
}
return ans;
}
int main(){
struct M a;
memset(unit.s,0,sizeof(unit.s));
char str[100];
int num[10];
for(int i=1;i<=30;i++)
unit.s[i][i]=1;
int h,z,p,cas,t;
int s,e,i,j,k;
scanf("%d",&cas);
while(cas--){
memset(a.s,0,sizeof(a.s));
scanf("%d %d",&h,&z);
n=h*z;
for(i=1;i<=h;i++)
for(j=1;j<=z;j++){
scanf("%s",str);
sscanf(str,"((%d,%d),(%d,%d),(%d,%d),(%d,%d))",&num[1],&num[2],&num[3],&num[4],&num[5],&num[6],&num[7],&num[8]);
s=(i-1)*z+j;
for(k=1;k<=8;k+=2){
e=(num[k]-1)*z+num[k+1];
a.s[s][e]=1;
}
}
//:转换成邻接矩阵后,a.s[n][]就是
//代表原来地图里的[n][m]点与其他点的链接状态
//因为题意说,凡是到了[n][m]点之后,就会马上
//全送出去,离开这个地图,所以我们要把[n][m]到其他点的
//状态值都赋为0!
for(i=1;i<=n;i++)
a.s[n][i]=0;
scanf("%d",&p);
while(p--){
scanf("%d",&t);
struct M c=paw(a,t);
if(c.s[1][n]==0)
printf("False\n");
else{
int x;
for(x=1;x<=n;x++){
if(c.s[1][x]==1)
break;
}
if(n==x)
printf("True\n");
else
printf("Maybe\n");
}
}
printf("\n");
}
}
HDU (1683 纪念SlingShot )
题目:已知 F(n)=3 * F(n-1)+2 * F(n-2)+7 * F(n-3),n>=3,其中F(0)=1,F(1)=3,F(2)=5,对于给定的每个n,输出F(0)+ F(1)+ …… + F(n) mod 2009。
题目分析:这里我们推出S[N]=S[N-1]+F[N];
F[N]=3*F[N-1] +2*F[N-2] +7*F[N-3];
首先我们要知道这点,我们这里在第推计算 F[n]的同时,也要计算出 S[N];
所以您要构造出一个矩阵 把S[N] F[N] 同时收录计算,在这里我构造的矩阵 如下:
由于第一写了很多,完成文章的时候莫名其妙的 成了空白,所以第二次 我没上次那么仔细分析了
您有不懂的 或者指点的地方 请留言 我立即修正 或者给您答疑:
模拟计算过程的矩阵;
1 3 2 7
0 3 2 7
0 1 0 0
0 0 1 0
初始状态的矩阵:
9 0 0 0
5 0 0 0
3 0 0 0
1 0 0 0
还有构造一个单位矩阵 unit用来 二分计算 {^_^}
代码+部分注释:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M {
int s[5][5];
};
struct M unit,tempt,res;
struct M multiply(struct M a,struct M b){
struct M c;
for(int i=1;i<=4;i++)
for(int j=1;j<=4;j++){
c.s[i][j]=0;
for(int k=1;k<=4;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%2009)%2009;
}
return c;
}
struct M paw(int t){
struct M ans=unit;
struct M a=tempt;
struct M b=res;
while(t){
if(t%2==1)
ans=multiply(ans,a);
a=multiply(a,a);
t/=2;
}
b=multiply(ans,b);
return b;
}
int main(){
int f[5];
f[1]=1; f[2]=3; f[3]=5;
f[4]=28;
memset(unit.s,0,sizeof(unit.s));
memset(res.s,0,sizeof(res.s));
memset(tempt.s,0,sizeof(tempt.s));
for(int i=1;i<=4;i++)
unit.s[i][i]=1;
tempt.s[1][1]=1; tempt.s[1][2]=3;
tempt.s[1][3]=2; tempt.s[1][4]=7;
tempt.s[2][2]=3; tempt.s[2][3]=2;
tempt.s[2][4]=7; tempt.s[3][2]=1;
tempt.s[4][3]=1;
res.s[1][1]=9; res.s[2][1]=5;
res.s[3][1]=3; res.s[4][1]=1;
int cas,t,k;
scanf("%d",&cas);
for(k=1;k<=cas;k++){
scanf("%d",&t);
t++;
if(t<=3){
int sum=0;
for(int i=1;i<=t;i++)
sum+=f[i];
printf("Case %d: %d\n",k,sum);
continue;
}
struct M c=paw(t-3);
printf("Case %d: %d\n",k,c.s[1][1]);
}
return 0;
}
FZU 1692(Key problem)
题目分析: 首先题目大意是,有n个小孩,初始时每个人有ai个苹果。现在要进行m轮游戏。每进行一轮游戏,第i个小孩的苹果增加
( R*A(i+n-1)%n+L*A(i+1)%n )个,求进行m轮游戏后,每个小孩有多少个苹果。(0<=m<=10^9,结果模M后输出,1<=M<=10^6)!注意原题目的公式是错的,害的我郁闷了好久~真的 faint!
思路分析:
这些都属于 循环同构的矩阵 计算的一个巧妙的算法就是,只算第一行,然后接下来的只要平移一个单位到下面,然后复制!
做这种题目还是要首先构造出一个矩阵 模拟他的递归过程!
我这里构造的矩阵是:
1 L .... R
R 1 L.. 0
0 R 1 L..0
L..... 0 R 1
然后递归多少次,我只要把这个矩阵乘多少次就可以了,这样做的高效远远优于递归的!
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M{
int s[101][101];
};
int n,p,t;
struct M tempt,unit,res;
//计算矩阵的幂的时候,因为我要计算的矩阵是 循环同构的
//所以只需要计算第一行,其他的N-1行只需要帮他上面一行的
//结果平移一个单位,然后再复制下来就OK啦!
struct M multiply(struct M a,struct M b){
struct M c;
int i,j,k;
for(i=1;i<=1;i++)
for(j=1;j<=n;j++){
c.s[i][j]=0;
for(k=1;k<=n;k++){
if(a.s[i][k]&&b.s[k][j])
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
}
}
for(i=2;i<=n;i++){
c.s[i][1]=c.s[i-1][n];
for(j=2;j<=n;j++)
c.s[i][j]=c.s[i-1][j-1];
}
return c;
}
struct M multiply2(struct M a,struct M b){
struct M c;
int i,j,k;
for(i=1;i<=n;i++)
for(j=1;j<=1;j++){
c.s[i][j]=0;
for(k=1;k<=n;k++){
if(a.s[i][k]&&b.s[k][j])
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
}
}
return c;
}
void paw(){
struct M ans=unit;
int i,j;
struct M a=tempt;
while(t){
if(t%2==1)
ans=multiply(ans,a);
a=multiply(a,a);
t/=2;
}
res=multiply2(ans,res);
}
int main(){
int cas,l,r,i,j;
int sim[102];
memset(unit.s,0,sizeof(unit.s));
for(i=1;i<=100;i++)
unit.s[i][i]=1;
cin>>cas;
while(cas--){
memset(res.s,0,sizeof(res.s));
memset(tempt.s,0,sizeof(tempt.s));
scanf("%d %d %d %d %d",&n,&t,&r,&l,&p);
for(i=1;i<=n;i++)
scanf("%d",∼[i]);
for(j=1,i=n;i>=1;j++,i--){
res.s[j][1]=sim[i];
}
tempt.s[1][1]=1; tempt.s[1][2]=l;
tempt.s[1][n]=r;
for(i=2;i<=n;i++){
tempt.s[i][1]=tempt.s[i-1][n];
for(j=2;j<=n;j++)
tempt.s[i][j]=tempt.s[i-1][j-1];
}
paw();
for(i=n;i>1;i--)
printf("%d ",res.s[i][1]);
printf("%d",res.s[i][1]);
printf("\n\n");
}
}
HDU (2276 Kiki & Little Kiki 2 )
题目大意:题目大意给定一系列灯的初始状态,0代表暗,1代表亮,每一秒所有的灯都有可能发生状态切换,
切换规则:当前灯的左边第一个灯是亮的,则当前的灯切换状态,如果当前灯的左边第一盏灯是暗的,则当前灯的状态无需变化!
注意:最左边的参考左右边那栈灯。
题目分析;
首先有两种情况:
左边第一盏灯亮的:
当前灯的动作: 1->0; 0->1;
左边第一盏灯暗的:
当前灯的动作:
1->1; 0->0;
我们可以看到的是, 可以用一个方程来模拟这个过程: F[i] = ( f [ i] +f [i+n-2]%n+1 )%2;
所以我们只要计算这个值就OK啦。
然后由于数据过大,开数组肯定会爆掉~
这里我们要想到的是 矩阵是一个模拟递归的高效算法
这里我们要构造一个 可以计算如上的方程的矩阵:
1 0 0...0 1
1 1 0...0 0
0 1 1..0 0
0 0 1..0 0
. . . 0 ....
. . .0.....
0 0 0..0 1
然后再把f[n]...到f[1]构成一个矩阵和他相乘,正好就是达到了表达式的效果。如果还有不懂的那请您留言,我这里画图不方便悲剧的很
代码+部分注释:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char sim[102];
struct M{
int s[101][101];
};
struct M unit,res,tempt;
int n,t;
struct M multiply(struct M a,struct M b){
struct M c;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++){
c.s[i][j]=0;
for(int k=1;k<=n;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%2)%2;
}
return c;
}
void paw(){
struct M ans=unit;
struct M a=tempt;
while(t){
if(t%2==1)
ans=multiply(ans,a);
a=multiply(a,a);
t/=2;
}
res=multiply(res,ans);
}
int main(){
int i,j,k;
memset(unit.s,0,sizeof(unit.s));
for(i=1;i<=100;i++)
unit.s[i][i]=1;
while(scanf("%d %s",&t,sim)!=EOF){
memset(tempt.s,0,sizeof(tempt.s));
memset(res.s,0,sizeof(res.s));
k=strlen(sim);
n=k;
for(i=1;i<=k;i++)
res.s[1][i]=sim[k-i]-'0';
for(i=1;i<=n;i++){
if(i!=n)
tempt.s[i][i]=tempt.s[i+1][i]=1;
else
tempt.s[1][n]=tempt.s[n][n]=1;
}
paw();
for(int i=n;i>=1;i--)
printf("%d",res.s[1][i]);
printf("\n");
}
return 0;
}
HDU 1757(A Simple Math Problem)
题目分析:
If x < 10 f(x) = x.
If x >= 10 f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10);
And ai(0<=i<=9) can only be 0 or 1 .
Now, I will give a0 ~ a9 and two positive integers k and m ,and could you help Lele to caculate f(k)%m.
In each case, there will be two lines.
In the first line , there are two positive integers k and m. ( k<2*10^9 , m < 10^5 )
In the second line , there are ten integers represent a0 ~ a9.
这里就是构造一下矩阵 然后依然是矩阵的多次幂 我前面说的很详细,如果看的不清楚可以看我别的文章
构造一个矩阵

就求a^(t-9)*b
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M {
int s[11][11];
};
int n,p;
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=10;i++)
for(int j=1;j<=10;j++)
for(int k=1;k<=10;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M b=paw(a,t/2);
if(t&1){
return multiply(multiply(b,b),a);
}
else
return multiply(b,b);
}
}
int main(){
struct M a,b,c;
int t;
memset(a.s,0,sizeof(a.s));
memset(b.s,0,sizeof(b.s));
for(int i=1;i<=10;i++)
b.s[i][1]=10-i;
for(int i=2;i<=10;i++)
a.s[i][i-1]=1;
while(scanf("%d %d",&t,&p)!=EOF){
for(int i=1;i<=10;i++)
scanf("%d",&a.s[1][i]);
if(t<=9){
printf("%d\n",t);
continue;
}
c=paw(a,t-9);
c=multiply(c,b);
printf("%d\n",c.s[1][1]);
}
return 0;
}
HDU (1575 Tr A)
题目分析:Tr A表示方阵A的迹(主对角线元素之和),求Tr(Ak) % 9973。
由于k最大有10^9,所以只能用矩阵二分快速幂得到Ak,最后求和即可。
代码:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M {
int s[11][11];
};
int n,p=9973;
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M b=paw(a,t/2);
if(t&1){
return multiply(multiply(b,b),a);
}
else
return multiply(b,b);
}
}
int main(){
struct M a,b;
int k,sum,cas;
cin>>cas;
while(cas--){
scanf("%d %d",&n,&k);
sum=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&a.s[i][j]);
/*for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
printf("%d",a.s[i][j]);*/
b=paw(a,k);
for(int i=1;i<=n;i++)
sum=(sum+b.s[i][i])%p;
printf("%d\n",sum);
}
return 0;
}
HDU (2855 Fibonacci Check-up)
题目大意:
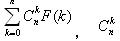 这个是组合数,然后求给定N,P让你求
这个是组合数,然后求给定N,P让你求![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) mod p的值是多少
mod p的值是多少
题目分析:
第一种方法:这里我引用一种常见的母函数:
(a+1)^n=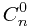 +
+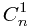 *a^1+
*a^1+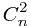 *a^2+....+
*a^2+....+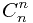 *a^n;
*a^n;
这里我可以知道fibonacci数可以用mitrax=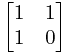 的乘积表示,f[i]=mitrax^i;
的乘积表示,f[i]=mitrax^i;
这里我们的“1”可以用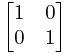 表示 即单位矩阵,这样我们只要求两个矩阵的的 i 次幂就可以了,这就直接转换到矩阵的二分法求快速幂上来了!注意一点,最后输出的[1][2]这个位置的数,别输出错了!
表示 即单位矩阵,这样我们只要求两个矩阵的的 i 次幂就可以了,这就直接转换到矩阵的二分法求快速幂上来了!注意一点,最后输出的[1][2]这个位置的数,别输出错了!
第二种方法:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) 最后证明结论等于:
最后证明结论等于:![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) = F[ 2* N ]
= F[ 2* N ]
引进fibonacci数的计算方程:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) ={
={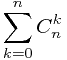 *(
*(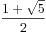 )^k -(
)^k -(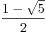 )^k}
)^k}
因为:
(a+1)^n=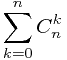 *a^k;
*a^k;
所以将上式化简成:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) =(
=(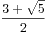 )^n+(
)^n+(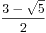 )^n
)^n
分子分母都乘*2 =(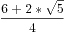 )^n+(
)^n+(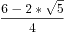 )^n
)^n
=(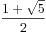 )^2n+(
)^2n+(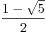 )^2n
)^2n
=F[ 2*N ]
我的代码是第一种的:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M {
int s[3][3];
};
int p;
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M b=paw(a,t/2);
if(t&1){
return multiply(multiply(b,b),a);
}
else
return multiply(b,b);
}
}
int main(){
struct M a,b;
int n,cas;
a.s[1][1]=2; a.s[1][2]=1;
a.s[2][1]=1; a.s[2][2]=1;
/*b.s[1][1]=1; b.s[1][2]=0;
b.s[2][1]=0; b.s[2][2]=1;*/
scanf("%d",&cas);
while(cas--){
scanf("%d %d",&n,&p);
if(n==0)
{ printf("0\n"); continue; }
b=paw(a,n);
printf("%d\n",b.s[1][2]);
}
return 0;
}
文章总结:(a+1)^n=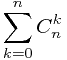 *a^k;这个母函数很好用 下次记得灵活运用!
*a^k;这个母函数很好用 下次记得灵活运用!
HDU 3117( Fibonacci Numbers 十大经典之二 :矩阵快速幂的应用)
题目大意:求
Fibonacci Numbers如果位数低于8位,则全部输出,否则只输出
前4位与后4位(注意后四位的0别忘记了,不过是什么格式,哪怕
0000都要输出);
题目分析:这里我们上一篇文章以前具体阐述了:
给定矩阵A,请快速计算出A^n(n个A相乘)的结果,输出的每个数都mod p。
由 于矩阵乘法具有结合律,因此A^4 = A * A * A * A = (A*A) * (A*A) = A^2 * A^2。我们可以得到这样的结论:当n为偶数时,A^n = A^(n/2) * A^(n/2);当n为奇数时,A^n = A^(n/2) * A^(n/2) * A (其中n/2取整)。这就告诉我们,计算A^n也可以使用二分快速求幂的方法。例如,为了算出A^25的值,我们只需要递归地计算出A^12、A^6、 A^3的值即可。根据这里的一些结果,我们可以在计算过程中不断取模,避免高精度运算。
然后我们以前有一篇文章已经阐述了,如果利用取对数求第N个fibonacci数的前4位有效数字;如果不清楚的话 请看我以前的一篇文章
“HDU 1568(非常经典微妙的 斐波纳契计算)“
代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
int sim[50]={0};
double f=(1+sqrt(5.0))/2;
double ff=(1-sqrt(5.0))/2;
struct M{
int s[5][5];
};
int solve_f4(int n){
double t=(-0.5)*log(5.0)/log(10.0)+(double(n))*log(f)/log(10.0);
double k=t-floor(t);
t=pow(10.0,k);
while(t<1000)
t*=10.0;
return (int)t;
}
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%10000)%10000;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M k=paw(a,t/2);
if(t&1){
return multiply(multiply(k,k),a);
}
else
return multiply(k,k);
}
}
int main(){
int n,k1,k2;
struct M a,b;
a.s[1][1]=1;
a.s[1][2]=0;
a.s[2][1]=0;
a.s[2][2]=1;
b.s[1][1]=b.s[1][2]=b.s[2][1]=1;
b.s[2][2]=0;
sim[0]=0;
sim[1]=1; sim[2]=1; sim[3]=2;
for(int i=4;i<=49;i++)
sim[i]=sim[i-2]+sim[i-1];
while(scanf("%d",&n)!=EOF){
if(n<=39){
printf("%d\n",sim[n]);
continue;
//其实我最初是用公式求前39个fibonacci数的
//但是发现有误差,所以改用数组直接模拟出来
}
else{
k1=solve_f4(n);
struct M k=paw(b,n-1);
k=multiply(k,a);
k2=k.s[1][1]%10000;
printf("%d...%04d\n",k1,k2);
}
}
return 0;
}
”
POJ 3070(Fibonacci )
题目分析:
经典题目6 给定n和p,求第n个Fibonacci数mod p的值,n不超过2^31
根 据前面的一些思路,现在我们需要构造一个2 x 2的矩阵,使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵,这两个数就会多迭代一次。那么,我们把这个2 x 2的矩阵自乘n次,再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想,这个2 x 2的矩阵很容易构造出来:
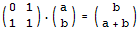
但是我这里稍微有点区别的是,我是构造: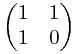 其实这里
其实这里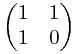 *
*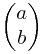 =
=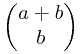
为了计算直观我把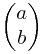 写成
写成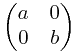 都一样的 其实 呵呵
都一样的 其实 呵呵
这里我们的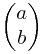 =
=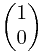
然后我们用二分的方法求矩阵的快速幂!
这里建议大家用结构体传递矩阵 这样很好用的!
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
struct M{
int s[5][5];
};
int p=10000;
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
c.s[i][j]=(c.s[i][j]+ (a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M c=paw(a,t/2);
if(t&1){
return multiply(c,multiply(c,a));
}
else{
return multiply(c,c);
}
}
}
int main(){
int n;
struct M a,d;
a.s[1][1]=a.s[1][2]=a.s[2][1]=1;
a.s[2][2]=0;
d.s[1][1]=1;
d.s[1][2]=0;
d.s[2][1]=0;
d.s[2][2]=1;
while(scanf("%d",&n),n!=-1){
if(n==0){
printf("0\n");
continue;
}
if(n==1||n==2){
printf("1\n");
continue;
}
struct M k=paw(a,n-1);
struct M b=multiply(d,k);
printf("%d\n",b.s[1][1]);
}
}
POJ 3233( 3233 Matrix Power Series 矩阵的快速幂 )
题目分析:
S = A + A2 + A3 + … + Ak.
求 S mod p;
我们要二分考虑
二分求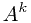 mod p
mod p
首先把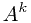 转化成:
转化成:
1) 如果k是偶数 (  mod p ) * (
mod p ) * (  mod p )这样就把就达到了降幂的作用
mod p )这样就把就达到了降幂的作用
2)如果k是奇数 (  mod p ) * (
mod p ) * (  mod p )* ( A mod p)
mod p )* ( A mod p)
然后再对求和的过程进行二分!
如果K是偶数我们把公式转换成 S=A + A2 + A3 + … +  +
+ *(A + A2 + A3 + … +
*(A + A2 + A3 + … +  )
)
如果K是奇数 则可以写成: S=A + A2 + A3 + … + 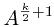 +
+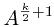 *(A + A2 + A3 + … +
*(A + A2 + A3 + … +  )
)
代码+部分注释:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M{
int s[32][32];
};
int n,p;
struct M add(struct M a,struct M b){
int i,j;
struct M c;
memset(c.s,0,sizeof(c.s));
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
c.s[i][j]=(a.s[i][j]+b.s[i][j])%p;
return c;
}
struct M multiply(struct M a,struct M b){
int i,j,k;
struct M c;
memset(c.s,0,sizeof(c.s));
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
for(k=1;k<=n;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
struct M b;
memset(b.s,0,sizeof(b.s));
if(t==0){
for(int i=1;i<=n;i++)
b.s[i][i]=1;
return b;
}
else{
struct M k=paw(a,t/2);
if(t&1){
return multiply(multiply(k,k),a);
}
else
return multiply(k,k);
}
}
struct M sum(struct M a,int t){
if(t==1){
return a;
}
else{
struct M tempt=sum(a,t/2);
if(t&1){
struct M k=paw(a,t/2+1);
return add(add(tempt,k),multiply(tempt,k));
}
else{
return add(tempt,multiply(tempt,paw(a,t/2)));
}
}
}
int main(){
int k,i,j;
struct M a;
cin>>n>>k>>p;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++){
scanf("%d",&a.s[i][j]);
a.s[i][j]%=p;
}
struct M tempt=sum(a,k);
for(i=1;i<=n;i++){
for(j=1;j<n;j++){
cout<<tempt.s[i][j]<<" ";
}
printf("%d\n",tempt.s[i][j]);
}
return 0;
}