POJ 3070(Fibonacci )

spoiler posted @ 2011年4月26日 04:40 in 十个利用矩阵乘法解决的经典题目 , 2159 阅读

题目分析：

经典题目6 给定n和p，求第n个Fibonacci数mod p的值，n不超过2^31
根据前面的一些思路，现在我们需要构造一个2 x 2的矩阵，使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵，这两个数就会多迭代一次。那么，我们把这个2 x 2的矩阵自乘n次，再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想，这个2 x 2的矩阵很容易构造出来：

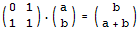
但是我这里稍微有点区别的是，我是构造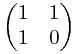： $\begin{pmatrix}1 & 1\\1 &0\end{pmatrix}$ 其实这里 $\begin{pmatrix}1 & 1\\1 &0\end{pmatrix}$ * $\begin{pmatrix}a\\b\end{pmatrix}$ = $\begin{pmatrix}a+b\\b\end{pmatrix}$

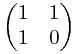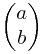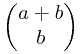
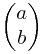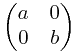为了计算直观我把 $\begin{pmatrix}a\\b\end{pmatrix}$ 写成 $\begin{pmatrix}a&0\\0&b\end{pmatrix}$ 都一样的其实呵呵

这里我们的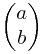 $\begin{pmatrix}a\\b\end{pmatrix}$ = $\begin{pmatrix}1\\0\end{pmatrix}$

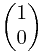
然后我们用二分的方法求矩阵的快速幂！

这里建议大家用结构体传递矩阵这样很好用的！

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
struct M{
	int s[5][5];
};
int p=10000;
struct M multiply(struct M a,struct M b){
	struct M c;
	memset(c.s,0,sizeof(c.s));
	for(int i=1;i<=2;i++)
		for(int j=1;j<=2;j++)
			for(int k=1;k<=2;k++)
				c.s[i][j]=(c.s[i][j]+ (a.s[i][k]*b.s[k][j])%p)%p;
	return c;
}
struct M paw(struct M a,int t){
	if(t==1)
		return a;
	else{
		struct M c=paw(a,t/2);
		if(t&1){
			return multiply(c,multiply(c,a));
		}
		else{
			return multiply(c,c);
		}
	}
}
int main(){
	int n;
	struct M a,d;
	a.s[1][1]=a.s[1][2]=a.s[2][1]=1;
	a.s[2][2]=0;
	d.s[1][1]=1;
	d.s[1][2]=0;
	d.s[2][1]=0;
	d.s[2][2]=1;
	while(scanf("%d",&n),n!=-1){
		if(n==0){
			printf("0\n");
			continue;
		}
		if(n==1||n==2){
			printf("1\n");
			continue;
		}
		struct M k=paw(a,n-1);
		struct M b=multiply(d,k);
		printf("%d\n",b.s[1][1]);
	}
}