POJ 3233( 3233 Matrix Power Series 矩阵的快速幂 )

spoiler posted @ 2011年4月25日 21:32 in 十个利用矩阵乘法解决的经典题目 , 2601 阅读

题目分析：

S = A + A² + A³ + … + A^k.

求 S mod p;

我们要二分考虑

二分求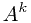 $$A^k$$ mod p

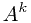首先把 $$A^k$$ 转化成：

1）如果k是偶数 ( $A^{\frac{k}{2}}$ mod p ) * ( $A^{\frac{k}{2}}$ mod p )这样就把就达到了降幂的作用

2）如果k是奇数 ( $A^{\frac{k}{2}}$ mod p ) * ( $A^{\frac{k}{2}}$ mod p )* ( A mod p)

然后再对求和的过程进行二分！

如果K是偶数我们把公式转换成 S=A + A² + A³ + … + $A^{\frac{k}{2}}$ + $A^{\frac{k}{2}}$ *（A + A² + A³ + … + $A^{\frac{k}{2}}$ ）

如果K是奇数则可以写成： S=A + A² + A³ + … + 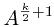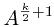$A^{\frac{k}{2}+1}$ + $A^{\frac{k}{2}+1}$ *（A + A² + A³ + … + $A^{\frac{k}{2}}$ ）

代码+部分注释：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M{
	int s[32][32];
};
int n,p;
struct M add(struct M a,struct M b){
	int i,j;
	struct M c;
	memset(c.s,0,sizeof(c.s));
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
			c.s[i][j]=(a.s[i][j]+b.s[i][j])%p;
	return c;
}
struct M multiply(struct M a,struct M b){
	int i,j,k;
	struct M c;
	memset(c.s,0,sizeof(c.s));
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++)
			for(k=1;k<=n;k++)
				c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
	return c;
}
struct M paw(struct M a,int t){
	struct M b;
        memset(b.s,0,sizeof(b.s));
	if(t==0){
		for(int i=1;i<=n;i++)
			b.s[i][i]=1;
		return b;
	}
	else{
		struct M k=paw(a,t/2);
		if(t&1){
			return multiply(multiply(k,k),a);
		}
		else
			return multiply(k,k);
	}
}
struct M sum(struct M a,int t){
	if(t==1){
		return a;
	}
	else{
		struct M tempt=sum(a,t/2);
		if(t&1){
			struct M k=paw(a,t/2+1);
			return add(add(tempt,k),multiply(tempt,k));
		}
		else{
			return add(tempt,multiply(tempt,paw(a,t/2)));
		}
	}
}
int main(){
	int k,i,j;
	struct M a;
	cin>>n>>k>>p;
	for(i=1;i<=n;i++)
		for(j=1;j<=n;j++){
			scanf("%d",&a.s[i][j]);
			a.s[i][j]%=p;
		}
	struct M tempt=sum(a,k);
	for(i=1;i<=n;i++){
		for(j=1;j<n;j++){
			  cout<<tempt.s[i][j]<<" ";
		}
		printf("%d\n",tempt.s[i][j]);
	}
	return 0;
}