hello kity
期待您的批阅,由于写解题报告时 不一定考虑的很周到,所以如果您有什么不懂的地方,请您留言,然而一天之内我肯定会看见您信息,再对代码注释详细,让您更好的阅读
分类
最新评论
最新留言
链接
RSS
计数器
224421
功能
HDU (2855 Fibonacci Check-up)
spoiler
posted @ 2011年4月26日 20:57
in 十个利用矩阵乘法解决的经典题目
, 1929 阅读
题目大意:
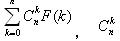 这个是组合数,然后求给定N,P让你求
这个是组合数,然后求给定N,P让你求![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) mod p的值是多少
mod p的值是多少
题目分析:
第一种方法:这里我引用一种常见的母函数:
(a+1)^n=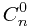 +
+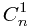 *a^1+
*a^1+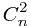 *a^2+....+
*a^2+....+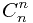 *a^n;
*a^n;
这里我可以知道fibonacci数可以用mitrax=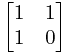 的乘积表示,f[i]=mitrax^i;
的乘积表示,f[i]=mitrax^i;
这里我们的“1”可以用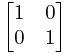 表示 即单位矩阵,这样我们只要求两个矩阵的的 i 次幂就可以了,这就直接转换到矩阵的二分法求快速幂上来了!注意一点,最后输出的[1][2]这个位置的数,别输出错了!
表示 即单位矩阵,这样我们只要求两个矩阵的的 i 次幂就可以了,这就直接转换到矩阵的二分法求快速幂上来了!注意一点,最后输出的[1][2]这个位置的数,别输出错了!
第二种方法:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) 最后证明结论等于:
最后证明结论等于:![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) = F[ 2* N ]
= F[ 2* N ]
引进fibonacci数的计算方程:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) ={
={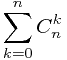 *(
*(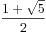 )^k -(
)^k -(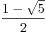 )^k}
)^k}
因为:
(a+1)^n=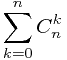 *a^k;
*a^k;
所以将上式化简成:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) =(
=(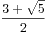 )^n+(
)^n+(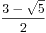 )^n
)^n
分子分母都乘*2 =(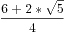 )^n+(
)^n+(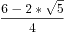 )^n
)^n
=(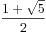 )^2n+(
)^2n+(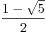 )^2n
)^2n
=F[ 2*N ]
我的代码是第一种的:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M {
int s[3][3];
};
int p;
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M b=paw(a,t/2);
if(t&1){
return multiply(multiply(b,b),a);
}
else
return multiply(b,b);
}
}
int main(){
struct M a,b;
int n,cas;
a.s[1][1]=2; a.s[1][2]=1;
a.s[2][1]=1; a.s[2][2]=1;
/*b.s[1][1]=1; b.s[1][2]=0;
b.s[2][1]=0; b.s[2][2]=1;*/
scanf("%d",&cas);
while(cas--){
scanf("%d %d",&n,&p);
if(n==0)
{ printf("0\n"); continue; }
b=paw(a,n);
printf("%d\n",b.s[1][2]);
}
return 0;
}
文章总结:(a+1)^n=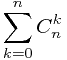 *a^k;这个母函数很好用 下次记得灵活运用!
*a^k;这个母函数很好用 下次记得灵活运用!
 评论 (0)
评论 (0)