FAFU 1079（帮东儿一个忙）经典素数的运用

题目大意：给你N，M，K让你求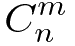里包含多少个k的倍数，也就是满足表达式

int Count (int 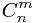, int k)
  {
   int ans = 0;
   while ( 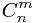%k == 0 )
   {
    ans ++;
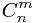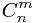     = / m;
   }
   return ans;
  }

 第一行一个整数t表示有t组测试数据，接下去每组三个整数n，m，k，其中 n，m，k < 10⁹ ,t < 10000 , k > 1。

题目思路：求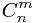里有多少个K的倍数，可以转换成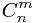里面的质因数是K的质因数的倍数的的最小值。

第一步：首先我们要枚举+筛选求出有可能成为K的质因数的 质数！在这里我们只需要枚举到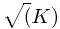并且只枚举奇数这样就大大优化了程序！

第二步：求出K的各个质因数的值和该质数出现的个数，分别存储在数组里，上限是枚举到pri[i]*pri[i]<=K;

第三步：根据已经求出的K的各个质因数和各个质因数在K里的个数，分别对每个质因数进行计算。

             目的是：我们求出这个质因数在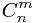里出现的次数！然后把出现的次数ans/vt[i]   ( vt[i]表示组成K的第i个质数在K里使用的次数 ) ，ans/vt[i]  也就是 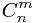里该质数出现的次数，是K里面出现次数的多少倍，也就是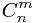里面有多少个该质数的倍数！

顺序枚举所有K的质因数，取ans/vt[i]最小的！

源程序+部分注释：

#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;
const int N=100000;
int pri[100000];
bool flag[100000];
int getprime(){
	int t=0,i,j,times;
	pri[++t]=2;
	for(i=1;i<=N;i++)
		flag[i]=1;
      //枚举到到N，也就是题目给出的最大值的开2次方！
	for(i=3;i<=N;i+=2){//只枚举奇数！
		if(flag[i]==1){
			pri[++t]=i;
                     //筛选求素数：
			for(j=i;j<=N;j+=i)
				flag[j]=0;
		}
	}
	return 0;
}

int des(int k,int* vs,int* vt){
	int t=0,i,times;
	for(i=1;pri[i]*pri[i]<=k;i++){
		times=0;
		while(k%pri[i]==0){
			times++;
			k/=pri[i];
		}
		if(times>0){
			vt[++t]=times;
			vs[t]=pri[i];	
		}
	}
	if(k!=1){
		vs[++t]=k;
		vt[t]=1;	
	}
	return t;
}

int add(int n,int t){
	int ans=0;
	while(n>=t){
		ans+=n/=t;
     //首先是能被t整除的，然后把n
    //附为n对t的倍数，也就是继续求
    //他的倍数的值里面还有多少个t的倍数！
	}
	return ans;
}

int cpt(int n,int m,int t,int ct){
	int tp=0;
	tp+=add(n,t);
	tp-=add(n-m,t);
	tp-=add(m,t);
	return tp/ct;
}

int main(){
	int cas,m,n,i,k;
	int Min=-1,ans,vs[100],vt[100];
	scanf("%d",&cas);
	getprime();
	while(cas--){
		scanf("%d %d %d",&n,&m,&k);
		Min=-1;
		int times=des(k,vs,vt);
		for(i=1;i<=times;i++){
			ans=cpt(n,m,vs[i],vt[i]);
			if(Min==-1||ans<Min)
				Min=ans;
		}
		printf("%d\n",Min);
	}
	return 0;
}