HDU 1131(Count the Trees)Catalan求树的构造方法数

题目大意：上面有一篇关于二叉树的构造方法数，这里只是普通的树，所以不用考虑次序。

Catalan数可以表示二叉树的构造方法数，Catalan数=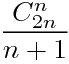 但是在这里我们不需要考虑次序，所以我们要乘以A(N,N);也就是N种元素的排列方法 也就是N！

所以这里的方法数=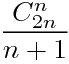*A（N，N）；

化简一下：

(n+2)*(n+3)*(n+4)*...*(2*n)

但是我这里直接把各个部分直接求出来的 嘿嘿，因为用JAVA写方便呀 所以都无所谓的啦

代码：

import java.io.*;
import java.util.Scanner;
import java.math.BigInteger;
public class Main{
			public static BigInteger C(int n,int m){
				BigInteger sum=BigInteger.valueOf(1);
				for(int i=n;i>n-m;i--)
					sum=sum.multiply(BigInteger.valueOf(i));
				for(int j=1;j<=m;j++)
					sum=sum.divide(BigInteger.valueOf(j));
				return sum;
			}
			public static BigInteger jie(int n){
				BigInteger sum=BigInteger.valueOf(1);
				for(int i=1;i<=n;i++)
					sum=sum.multiply(BigInteger.valueOf(i));
				return sum;
			}
			public static void main(String args[]){
				int n;
				Scanner cin=new Scanner(System.in);
				while(cin.hasNext()){
					n=cin.nextInt();
					if(n==0)
						break;
				BigInteger t1=C(2*n,n);
				BigInteger t2=jie(n);
				t1=t1.divide(BigInteger.valueOf(n+1));
				t1=t1.multiply(t2);
				System.out.println(t1);
				}
			}
}