hit2813 Garden visiting 关于组合数的一个简单的拆分求解

spoiler posted @ 2011年5月05日 16:57 in 数论 , 1730 阅读

题目大意：给你n * k 的矩形，始点在矩形的左上角，出口在矩形的右下角，求出最快走出这个矩阵的，方案数。

题目分析：最短的走出矩阵的方案的路程肯定是N+k，然后我们把这个路程离散化成N+K个状态，但是每种走法，的起点，跟终点的状态都一样的，只不过N+K-2里面有不同的走法，我们换位思考一下，在N+K-2个状态里有有K-1个状态分别投影在 K边的不同的点上面，因为，你必须往下移动K-1个单位才能到达出口，所以在竖直方向上必须有K-1个状态分别投影在K边的不同点上，这样我们就得出了方案数的组合数，就是在N+K-2里面选k-1个！公式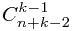： $C_{n+k-2}^{k-1}$

计算方面就是把这个组合数分别分解成素数，然后对素数进行求解，取模！

代码+部分注释：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int pri[20000],num[20000],cnt,p;
bool flag[200001];
void get_pri(){
    memset(flag,true,sizeof(flag));
    int i,j;
    pri[1]=2;
    cnt=1;
    for(i=4;i<=200000;i+=2)
        flag[i]=false;
    for(i=3;i<=3000;i+=2)
        for(j=i*i;j<=200000;j+=2*i)
            flag[j]=false;
    for(i=3;i<=200000;i+=2)
        if(flag[i])
            pri[++cnt]=i;
    return ;
}
int paw(int a,int t){
    int ans=1;
    while(t){
        if(t%2==1)
            ans=(ans*a)%p;
        a=(a*a)%p;
        t/=2;   
    }
    return ans;
}
int solve(){
    int cas,n,k,c,s,i;
    long long ans;
    scanf("%d",&cas);
    while(cas--){
        scanf("%d %d %d",&k,&n,&p);
        if(k>n){
            c=k;    k=n;
            n=c;
        }
        n=k+n-2;
        k--;
        if(k==n){
            printf("%d\n",1%p);
            continue;
        }
        for(i=1;i<=n&&pri[i]<=n;i++)
            num[i]=0;
        for(i=1;pri[i]<=n&&i<=cnt;i++){
            s=pri[i];
            while(n>=s){
                num[i]+=n/s-(n-k)/s-k/s;
                s*=pri[i];
            }
        }
        ans=1;
        for(i=1;i<=cnt&&pri[i]<=n;i++){
            if(num[i]>0)
                ans=(ans*paw(pri[i],num[i]))%p;
            if(ans==0)
                break;
        }
        printf("%lld\n",ans);
    }
    return 0;
}
int main(){
    get_pri();
    solve();
    return 0;
}