HDU 1222（Wolf and Rabbit）约瑟夫最小公倍数问题

spoiler posted @ 2011年4月18日 21:53 in 规律及递归经典题 , 2588 阅读

Problem Description

There is a hill with n holes around. The holes are signed from 0 to n-1.

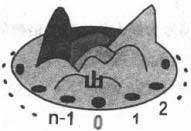A rabbit must hide in one of the holes. A wolf searches the rabbit in anticlockwise order. The first hole he get into is the one signed with 0. Then he will get into the hole every m holes. For example, m=2 and n=6, the wolf will get into the holes which are signed 0,2,4,0. If the rabbit hides in the hole which signed 1,3 or 5, she will survive. So we call these holes the safe holes.

Input

The input starts with a positive integer P which indicates the number of test cases. Then on the following P lines,each line consists 2 positive integer m and n(0<m,n<2147483648).

Output

For each input m n, if safe holes exist, you should output "YES", else output "NO" in a single line.

Sample Input

2
1 2
2 2

Sample Output

NO
YES

题目分析：

假设步长是m 总长度是N, 这里首先我们计算出他们的周期，也就是最小公倍数，当过了这个周期，狼搜索的点肯定重复了！

因为狼每走一次肯定是搜索了一个点，搜索完n个点的时候，走的长度正好是这个周期，说明他没有重复的搜索了N个点！你可以在纸上画一下

其实不难理解！

代码如下：

#include<iostream>
#include<cstdio>
using namespace std;
int gcd(int x,int y){
	int c;
	if(x<y){
		c=x;	x=y;
		y=c;
	}
	if(y==0)
		return x;
	else
		return gcd(y,x%y);
}
int main(){
	int cas,n,m;
	scanf("%d",&cas);
	while(cas--){
		scanf("%d %d",&m,&n);
		printf(gcd(n,m)==1?"NO\n":"YES\n");
	}
	return 0;
}

[回复]

전설 서구 说:
2021年4月03日 21:20

I appreciate this article for the well-researched content and excellent wording. I got so interested in this material that I couldn’t stop reading. Your blog is really impressive. gogoanime