POJ （1811 Prime Test 关于miller_rabin的素数判断和pollard_rho的整数分解）

题目大意：就是给一个很大的数，让你判断是否为素数，如果不是则计算出小于等于他的最小的素数。2 <= N < 2⁵⁴

题目分析： 这里由于数字非常大，我们不能按照常规思路来做，

miller_rabin的素数判断：Fermat小定理：若n为素数，则,有an-1≡1(mod n)，大部分的都满足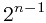=1(mod n)，但是这不能包含所有情况，所以我们利用随机函数，来随机产生在2～n-2直接的数进行测试，如果没测出来，几乎就可以判断这个数是素数，这样做n太大了，计算起来肯定会超时的，要知道n的范围：2～2^54 这样太可怕了，这样的话我们来优化：

首先n-1= m*2^q ，2^(n-1)=(2^m)^2^q 在这里求m,与q应该是非常简单的事情吧，然后我们怎么办呢？这里我可以利用随机数a枚举

(2^m)^2^q   （q=1..q-1），因为这些式子是 2^(n-1)的因数，如果他们不是素数，那么证明N不是素数，反之是素数（只是说概率很大可以 看作是了），

这里还有一种情况，就是该数不是素数，然后就要分解整数，求出最小的一个素数，这里分解整数，用到的是pollard_rho分解法：

这里证明我就不写了，水平有限，只写过程：

首先我们用随机函数生成一个x1（1<x1<n）,然后根据x1 构造出x2 ( f[x]=x1^2+c  )然后 这里假设有p 能够整除 x1-x2 ，x1-x2=p*q,这里q显然可以整除x1-x2，但是x1-x2不能整除n，从而可以得到，q不能整除 n，所以gcd( (x1-x2) ,n )有可能得到1，也有可能得到n的一个因数，所以我们进行随机枚举，这样就可以计算出n的因数分解形式。

代码+部分注释：

#include<iostream>
#include<cstdio>
#include<ctime>
 #include<cstdlib>
using namespace std;
long long top=0,pri[100];
long long multiply( long long a,long long b,long long n){
	long long exp,res=0;
        //这个就是用加法，来模拟乘法，为了防止运算的数太大，
	exp=a%n;
	while(b){
		if(b&1){
			res+=exp;
			if(res>n)
				res-=n;
		}
		exp<<=1;
		if(exp>n)
			exp-=n;
		b/=2;
	}
	return res;
}
long long paw(long long a,long long t,long long n){
	long long ans=1;
	a=a%n;
	while(t){
		if(t%2==1)
			ans=multiply(ans,a,n);	
		a=multiply(a,a,n);
		t/=2;
	}
	return ans;
}
long long gcd(long long a,long long b){
	long long c;
	if(a<b){
		c=a;
		a=b;	b=c;	
	}
	while(b){
		c=b;
		b=a%b;
		a=c;
	}
	return a;
}
bool miller_rabin(long long n,long long ti){
	if(n==2)
		return true;
	if(n<2||!(n&1))
		return false;
	long long p=n-1;
	long long k=0,a,x;
	while(p%2==0){
		p/=2;
		k++;
	}
	long long ans;
	srand(time(0));
	for(int t=1;t<=ti;t++){
		a=rand()%(n-1)+1;
		x=paw(a,p,n);
		for(int i=1;i<=k;i++){
			ans=multiply(x,x,n);
			if(ans==1&&x!=1&&x!=n-1)
				return false;
			x=ans;
		}
		if(ans!=1)
                //注意这个判断！
			return false;
	}
	return true;
}
long long pollard_rho(long long a,long long k,long long n){
	srand(time(0));
	long long x=rand()%(n-1)+1;
	long long i=1,t=2;
	long long y=x;
	while(1){
		i++;
		x=(multiply(x,x,n)+k)%n;
		long long ans=gcd(y-x,n);
		if(ans>1&&ans<n)
			return ans;
		if(x==y)
			return n;
		if(t==i){
			y=x;
			t*=2;
		}
	}
}
void search(long long n,long long k){
	if(miller_rabin(n,10)){
		pri[++top]=n;
		return ;
	}
	else{
		long long p=n;
		while(p>=n)
			p=pollard_rho(p,k--,n);
		search(p,k);
		search(n/p,k);
	}
}
int main(){
	int cas,i;
	long long n;
	cin>>cas;
	while(cas--){
		scanf("%lld",&n);
		if(miller_rabin(n,10ll))
			printf("Prime\n");
		else{	
			top=0;
			search(n,180);
			long long min=-1;
			for(i=1;i<=top;i++){
				if(min<0||min>pri[i])
					min=pri[i];
			}
			printf("%lld\n",min);
		}
	}
	return 0;
}