PKU （2992 Divisors 整数分解的经典应用！）

题目大意：就是给你一个组合数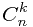 这里0=<k=<n=<341

题目分析：

1.约数个数定理：

                   设n的标准质因数分解为n=p1^a1*p2^a2*...*pm^am,

                    则n的因数个数=(a1+1)*(a2+1)*...*(am+1).

2. 对于任意质数p，n！中有（n/p+n/p^2+n/p^3+...)个质因子p。

代码+部分注释：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int pri[200];
bool flag[532];
int cnt;
void get_pri(){
	for(int i=1;i<=431;i++)
		flag[i]=true;
	pri[1]=2;
	cnt=1;
	flag[0]=flag[1]=false;
	for(int i=4;i<=431;i+=2)
		flag[i]=false;
	for(int i=3;i<23;i+=2)
		for(int j=i*i;j<=431;j+=2*i)
			flag[j]=false;
	for(int i=3;i<=431;i+=2)
		if(flag[i])
			pri[++cnt]=i;
	return ;
}
int main(){
	int n,k,s,i;
	int num[100];
	get_pri();
	while(scanf("%d %d",&n,&k)!=EOF){
		memset(num,0,sizeof(num));
		for(i=1;i<=cnt;i++){
			s=n;
			if(s<pri[i])
				break;
			while(s){
				num[i]+=s/pri[i];
				s/=pri[i];
			}
		}
		for(i=1;i<=cnt;i++){
			s=n-k;
			if(s<pri[i])
				break;
			while(s){
				num[i]-=s/pri[i];
				s/=pri[i];
			}
		}
		for(i=1;i<=cnt;i++){
			s=k;
			if(s<pri[i])
				break;
			while(s){
				num[i]-=s/pri[i];
				s/=pri[i];
			}
		}
		long long sum=1;
		for(i=1;i<=cnt;i++)
			if(num[i]>0)
				sum*=num[i]+1;
		printf("%lld\n",s);
	}
	return 0;
}