spoiler's Blog

hello kity

期待您的批阅，由于写解题报告时不一定考虑的很周到，所以如果您有什么不懂的地方，请您留言，然而一天之内我肯定会看见您信息，再对代码注释详细，让您更好的阅读

分类

HDU 1496（求多次方程的个数）

题目意思很好理解，就是求有多少种方程的解的形式，输出来就可以了。

如果用4重循环的话，可能会超时，没有试过。。直接用hash一一对应就可以了。

2重循环把s = a*x1*x1+b*x2*x2 看做一个数组的下标，直接hash[1000000+s]++；

再2重循环把s = c*x3*x3+d*x4*x4 看做下标，开始查找，如果有hash[1000000-s]跟他对应，说明他们两个值加起来等于0，即为方程的解。因为解可正可负，所以最后要乘16（2的四次方）！

代码+部分注释：

#include<iostream>
#include<cstring>
#include<stdio.h>
using namespace std;
int a,b,c,d,ans;
int s[2000000];
int solve(){
	int i,j;
	if((a>=0&&b>=0&&c>=0&&d>=0)||(a<=0&&b<=0&&c<=0&&d<=0))
		return 0;
	 memset(s,0,sizeof(s));
       //初始化放在这里 可以避免TLE因为，如果解不合法就没必要
        //初始化，7位数的初始化 很可怕的！
	for(i=1;i<=100;i++)
		for(j=1;j<=100;j++)
			s[1000000+(a*i*i+b*j*j)]+=1;
	for(i=1;i<=100;i++)
		for(j=1;j<=100;j++)
			ans+=s[1000000-(c*i*i+d*j*j)];
	return 0;
}
int main(){
	while(scanf("%d %d %d %d",&a,&b,&c,&d)!=EOF){
		ans=0;
		solve();	
		printf("%d\n",ans*16);
	}
	return 0;
}

HDU 1497（Simple Library Management System）

题目大意：图书管管理系统，有三个操作，一个借书，还书，查询。

优化方案：就是一个数组存放书的信息，下标为书的代号，内容存，0或者借走这本书的同学学号，这样可以方便查询！

#include<stdio.h>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

int stu,n;

struct node{
	int num;
	int t[15];
}s[1010];

int book[100005];

void init(){
	for(int i=1;i<=stu;i++){
		memset(s[i].t,0,sizeof(s[i].t));
		s[i].num=0;
	}
	memset(book,0,sizeof(book));
}
int cmp(int x,int y){
	return x<y;
}

int main(){
	int i,j,times;
	int x,y;
	char ch;
	while(~scanf("%d %d",&stu,&n)){
		scanf("%d",×);
		init();
		while(times--){
			j=0;
			getchar();
			scanf("%c",&ch);
			if(ch=='R'){
				scanf("%d",&x);
				if(book[x]!=0){
					printf("Return success\n");
					for(i=1;i<=9;i++){
						if(s[book[x]].t[i]==x)
							s[book[x]].t[i]=0;	
					}				
					s[book[x]].num--;
					book[x]=0;			
				}
				else
					printf("The book is already in the library\n");
				
			}
			else if(ch=='B'){
				scanf("%d %d",&x,&y);
				if(book[y]!=0){
                                 //这个地方一定得注意！因为这个WA了N次，题目说了
                                 //这个有先后顺序的，先判断书在么，再判断该同学借了9本了没
					printf("The book is not in the library now\n");
				}
				else if(s[x].num==9){
					printf("You are not allowed to borrow any more\n");
				}
				else{
					printf("Borrow success\n");
					sort(s[x].t,s[x].t+10,cmp);
					s[x].t[1]=y;
					s[x].num++;
					book[y]=x;
				}
					
			}
			else{
				scanf("%d",&x);
				sort(s[x].t,s[x].t+10,cmp);
				if(s[x].num==0)
					printf("Empty");
				//cout<<"???"<<endl;
				if(s[x].num!=0){
					for(i=1;i<=9;i++)
						if(s[x].t[i]!=0){
							printf(j==0?"%d":" %d",s[x].t[i]);
							j++;
						}
				}
				printf("\n");
			}
		}
		printf("\n");
		
	}
	return 0;
}

POJ 2409（Let it Bead）

题目分析：给你颜色数量，然后给你项链的长度，求能够染成多少种颜色。

题目分析：旋转：每转i个循环节就有gcd（n,i）个。

翻转：代会继续。。。比赛先

USTC 1151（Shortest Subsequence）

题目大意：题意很简单,就是在一串数字中找到一个子串,使得这个子串包含 1~n 的每一个数至少一次且长度最短。解法复
杂度是 O(n)的,做一次从左往右的扫描即可
题目分析：这道题刚开始不知道怎么做，后来请教别人然后看完解题报告终于明白这个精妙的维护过程！

首先在sim[]数组里存放各个输入的数据，flag[i],表示i在子串里出现的次数！然后用两个指标i,j分别从第一位扫描！

在这里j是代表一个子串的开头，i代表一个子串的结尾，用i遍历完一次就可以求出最短子串，

for i : 1->t

1）如果sim[i]是1~n里的数，进一步判断他是不是第一次出现在这个子串里，如果是total++（total是记录有多少个1～n里的数出现过的变量）

然后把 flag [ sim[ i ] ] + 1(不管是不是第一次出现，这里都要+1！),

2) 在j不超过i的前提下，对j的位置进行优化，首先如果j位上的数在子串里出现了2次或者2次以上说明我们最短子串里不需要包括

j位上的数，把j向右移动一位。

3）判断子串里是不是包括里所有1~m里的数，并且判断这个子串的长度是不是比上一个满足条件的子串短，如果两个条件都满足，我们分别更新记录最短子串的开头和结尾的两个变量：sn,en；

源程序+部分注释：

#include<iostream>
#include<cstdio>
using namespace std;

int sim[1000020],n,t;

bool init(){
	scanf("%d %d",&n,&t);
	if(n==0&&t==0)
		return false;
	for(int i=1;i<=t;i++)
		scanf("%d",∼[i]);
	return true;
}

void solve(){
	int i,j,sn,en,total;
	sn=1;	en=t;
	int flag[5020]={};
	total=0;
	for(i=1,j=1;i<=t;i++){
		if(sim[i]>=1&∼[i]<=n){
			if(flag[sim[i]]++==0)
				total++;
		}
		while(j<=i){
			if(flag[sim[j]]==1)
				break;
			flag[sim[j]]--;
			j++;
		}
		if(total==n&&i-j<en-sn){
			sn=j;
			en=i;
		}
	}
	if(en==t)
		printf("-1\n");
	else
		printf("%d %d\n",en-sn+1,en);
}

int main(){
	while(init()){
		solve();
	}
	return 0;
}

FAFU 1079（帮东儿一个忙）经典素数的运用

题目大意：给你N，M，K让你求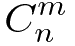 $$C_n^m$$ 里包含多少个k的倍数，也就是满足表达式

int Count (int 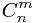$$C_n^m$$ , int k)
{
int ans = 0;
while ( 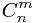%k == 0 )
{
ans ++;
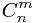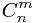= / m;
}
return ans;
}

第一行一个整数t表示有t组测试数据，接下去每组三个整数n，m，k，其中 n，m，k < 10⁹ ,t < 10000 , k > 1。

题目思路：求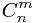 $$C_n^m$$ 里有多少个K的倍数，可以转换成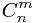里面的质因数是K的质因数的倍数的的最小值。

第一步：首先我们要枚举+筛选求出有可能成为K的质因数的质数！在这里我们只需要枚举到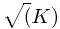 $\sqrt(K)$ 并且只枚举奇数这样就大大优化了程序！

第二步：求出K的各个质因数的值和该质数出现的个数，分别存储在数组里，上限是枚举到pri[i]*pri[i]<=K;

第三步：根据已经求出的K的各个质因数和各个质因数在K里的个数，分别对每个质因数进行计算。

目的是：我们求出这个质因数在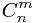 $$C_n^m$$ 里出现的次数！然后把出现的次数ans/vt[i] ( vt[i]表示组成K的第i个质数在K里使用的次数 ) ，ans/vt[i] 也就是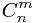里该质数出现的次数，是K里面出现次数的多少倍，也就是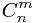里面有多少个该质数的倍数！

顺序枚举所有K的质因数，取ans/vt[i]最小的！

源程序+部分注释：

#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;
const int N=100000;
int pri[100000];
bool flag[100000];
int getprime(){
	int t=0,i,j,times;
	pri[++t]=2;
	for(i=1;i<=N;i++)
		flag[i]=1;
      //枚举到到N，也就是题目给出的最大值的开2次方！
	for(i=3;i<=N;i+=2){//只枚举奇数！
		if(flag[i]==1){
			pri[++t]=i;
                     //筛选求素数：
			for(j=i;j<=N;j+=i)
				flag[j]=0;
		}
	}
	return 0;
}

int des(int k,int* vs,int* vt){
	int t=0,i,times;
	for(i=1;pri[i]*pri[i]<=k;i++){
		times=0;
		while(k%pri[i]==0){
			times++;
			k/=pri[i];
		}
		if(times>0){
			vt[++t]=times;
			vs[t]=pri[i];	
		}
	}
	if(k!=1){
		vs[++t]=k;
		vt[t]=1;	
	}
	return t;
}

int add(int n,int t){
	int ans=0;
	while(n>=t){
		ans+=n/=t;
     //首先是能被t整除的，然后把n
    //附为n对t的倍数，也就是继续求
    //他的倍数的值里面还有多少个t的倍数！
	}
	return ans;
}

int cpt(int n,int m,int t,int ct){
	int tp=0;
	tp+=add(n,t);
	tp-=add(n-m,t);
	tp-=add(m,t);
	return tp/ct;
}

int main(){
	int cas,m,n,i,k;
	int Min=-1,ans,vs[100],vt[100];
	scanf("%d",&cas);
	getprime();
	while(cas--){
		scanf("%d %d %d",&n,&m,&k);
		Min=-1;
		int times=des(k,vs,vt);
		for(i=1;i<=times;i++){
			ans=cpt(n,m,vs[i],vt[i]);
			if(Min==-1||ans<Min)
				Min=ans;
		}
		printf("%d\n",Min);
	}
	return 0;
}

检查站（线段树）

#include<iostream>
#include<stdio.h>
using namespace std;

struct node{
	int r,l,Max;
}s[1000400];

void Build(int x,int y,int num){
	s[num].l=x;
	s[num].r=y;
	s[num].Max=0;
	if(x==y)
		return;
	int mid=(x+y)>>1;
	Build(x,mid,num+num);
	Build(mid+1,y,num+num+1);
}
int modify(int pos,int count,int num){
	if(s[num].l==s[num].r&&s[num].l==pos){
		s[num].Max=count;
	}
	else{
		int mid=(s[num].l+s[num].r)/2;
		if(pos<=mid)
			modify(pos,count,num+num);
		else 
			modify(pos,count,num+num+1);
		s[num].Max=max(s[num+num].Max,s[num+num+1].Max);
	}
}

int main(){
	int cas,i,x;
	int times=1;
	char ch[10];
	scanf("%d",&cas);
	int sn=1;
	int tn=1;
	Build(1,100000,1);
	while(cas--){
		scanf("%s",ch);
		if(ch[0]=='I'){
			scanf("%d",&x);
			modify(tn,x,1);
			tn++;
		}
		else if(ch[0]=='Q'){
			int ans=s[1].Max;
			printf("%d\n",ans);
		}
		else{
			modify(sn,0,1);
			sn++;
		}
	}
	return 0;
#include<iostream>
#include<stdio.h>
using namespace std;

struct node{
	int r,l,Max;
}s[1000400];

void Build(int x,int y,int num){
	s[num].l=x;
	s[num].r=y;
	s[num].Max=0;
	if(x==y)
		return;
	int mid=(x+y)>>1;
	Build(x,mid,num+num);
	Build(mid+1,y,num+num+1);
}
int modify(int pos,int count,int num){
	if(s[num].l==s[num].r&&s[num].l==pos){
		s[num].Max=count;
	}
	else{
		int mid=(s[num].l+s[num].r)/2;
		if(pos<=mid)
			modify(pos,count,num+num);
		else 
			modify(pos,count,num+num+1);
		s[num].Max=max(s[num+num].Max,s[num+num+1].Max);
	}
}

int main(){
	int cas,i,x;
	int times=1;
	char ch[10];
	scanf("%d",&cas);
	int sn=1;
	int tn=1;
	Build(1,100000,1);
	while(cas--){
		scanf("%s",ch);
		if(ch[0]=='I'){
			scanf("%d",&x);
			modify(tn,x,1);
			tn++;
		}
		else if(ch[0]=='Q'){
			int ans=s[1].Max;
			printf("%d\n",ans);
		}
		else{
			modify(sn,0,1);
			sn++;
		}
	}
	return 0;
}}

POJ 2777（Count Color）经典染色问题

题目大意：就是给出两种指令操作，
1. "C A B C" Color the board from segment A to segment B with color C.
2. "P A B" Output the number of different colors painted between segment A and segment B (including).

题目分析：首先建树，树节点有三个域，分别为左右端点r,l,与代表颜色的color。首先声明，当color等于0的时候表示被多种颜色覆盖了。

更新：首先如果在查找的过程中遇到当前区间的颜色大于0，也就是说这个区间已经被完全染色过，那么就把这个区间的颜色值往下传递，然后把这个区间的颜色值color赋值为0，继续往下查找，也就是常规的三种情况：左子树，右子树，或者左右子树混合的

直到当前区间的跟我的所要更新的区间吻合，停止往下更新！进行染色，也就是把color值附给他，还有一种情况就是：当前区间的color值大于0并且等于我所要染色的颜色值，这样也可以停止往下更新！

计数：在往下计数的时候，如果遇到color值大于0的直接把他在hash[]表里的映射赋值为1，这样防止重复计数！如果color==0；就继续往下计数。又是常规的三种情况！

源程序+部分注释：

#include<iostream>
#include<string.h>
#include<algorithm>
#include<stdio.h>
using namespace std;

struct node{
	int a,b,color;
}s[400000];
int h[60];
int Build(int x,int y,int num){
	s[num].a=x;	s[num].b=y;
	s[num].color=1;
	if(x==y)
		return 0;
	else{
		Build(x,(x+y)/2,num+num);
		Build((x+y)/2+1,y,num+num+1);
	}
}

int modify(int x,int y,int num,int color){
	if(x==s[num].a&&y==s[num].b){
		s[num].color=color;
		return 0;
	}
	if(s[num].color==color)
		return 0;
	if(s[num].color>0){
		s[num+num].color=s[num+num+1].color=s[num].color;
		s[num].color=0;
	}	
	if(y<=(s[num].a+s[num].b)/2)
		modify(x,y,num+num,color);
	else if(x>(s[num].a+s[num].b)/2)
		modify(x,y,num+num+1,color);
	else{
		modify(x,(s[num].a+s[num].b)/2,num+num,color);
		modify((s[num].a+s[num].b)/2+1,y,num+num+1,color);
	}
}

int getsum(int x,int y,int num){
	if(s[num].color>0){
		h[s[num].color]=1;
		return 0;
	}
	else{
		if(y<=(s[num].a+s[num].b)/2)
			getsum(x,y,num+num);
		else if(x>(s[num].a+s[num].b)/2)
			getsum(x,y,num+num+1);
		else{
			getsum(x,(s[num].a+s[num].b)/2,num+num);
			getsum((s[num].a+s[num].b)/2+1,y,num+num+1);
		}
	}
}

int main(){
	int l,t,cas,i,j,sum;
	int x,y,color;
	char c;
	scanf("%d %d %d",&l,&t,&cas);
		memset(h,0,sizeof(h));
		Build(1,l,1);
		for(j=1;j<=cas;j++){
			sum=0;
			cin>>c;
			if('P'==c){
				scanf("%d %d",&x,&y);
				getsum(x,y,1);
				for(i=1;i<=t;i++)
					cout<<h[i];
				cout<<endl;
				for(i=1;i<=t;i++)
					sum+=h[i];
				printf("%d\n",sum);
				memset(h,0,sizeof(h));
			}
			else if('C'==c){
				scanf("%d %d %d",&x,&y,&color);
				modify(x,y,1,color);
			}
		}
	return 0;
}

HDU 1394(Minimum Inversion Number)

题目大意：给你一个连续的自然数序列，
a1, a2, ..., an-1, an (where m = 0 - the initial seqence)
a2, a3, ..., an, a1 (where m = 1)
a3, a4, ..., an, a1, a2 (where m = 2)
...
an, a1, a2, ..., an-1 (where m = n-1)

中逆序数最大的是多少。

其实用树状数组求这个是非常方便速度的，但是为了锻炼线段树我还是用线段树写了。

程序+部分注释：

#include<iostream>
#include<stdio.h>
using namespace std;
int ans=0;
struct node{
	int a,b;
	int v;
}s[20000];

int t[5002];

int Build(int x,int y,int num){
	s[num].a=x;	s[num].b=y;
	s[num].v=0;
	if(x==y)
		return 0;
	Build(x,(s[num].a+s[num].b)/2,num+num);
	Build((s[num].a+s[num].b)/2+1,y,num+num+1);	
}

int modify(int num,int ide ){
	if(s[num].a==s[num].b){
		s[num].v=1;
		return 0;
	}
	else{
		if(ide<=(s[num].a+s[num].b)/2)
			modify(num+num,ide);
		else if(ide>(s[num].a+s[num].b)/2)
			modify(num+num+1,ide);
		s[num].v=s[num+num].v+s[num+num+1].v;
	}
}

int getsum(int x,int y,int num){
	if(x==s[num].a&&y==s[num].b){
		ans+=s[num].v;
		return 0;
	}
	else{
		if(y<=(s[num].a+s[num].b)/2)
			getsum(x,y,num+num);
		else if(x>(s[num].a+s[num].b)/2)
			getsum(x,y,num+num+1);
		else{
			getsum(x,(s[num].a+s[num].b)/2,num+num);
			getsum((s[num].a+s[num].b)/2+1,y,num+num+1);
		}
	}
}

int main(){
	int n,i,min;
	while(scanf("%d",&n)!=EOF){
		ans=0;
		for(i=1;i<=n;i++)
			scanf("%d",&t[i]);
		Build(1,n,1);
		for(i=n;i>=1;i--){
			getsum(1,t[i]+1,1);
			modify(1,t[i]+1);
                        求出总和
		}
		min=ans;
		for(i=1;i<=n-1;i++){
			ans=ans-t[i]+n-t[i]-1;
                        //因为数组是连续的自然数，从0到n所以
                       //t[i]移动到最后面去，就减少了t[i]个逆                    
                         //序对，同时也与以前是后面的而且比他大的数构成了
                           //N-（t[i]+1）组逆序对
			if(ans<min)
				min=ans;
		}
		printf("%d\n",min);
	}
	return 0;
}

HDU 1698（Just a Hook）

题目大意：给一组棍子染色，不同的颜色有不同的值，执行一系列的区间染色后，问这组棍子的总值是多少。

题目分析：建树：节点的域有左右节点和颜色，a,b,v；v=0时表示这个区间由多种颜色覆盖。

更新的时候，如果更新区间比当前区间小，并且当前区间的颜色大于0，说明已经被完全染色，就把该区间颜色传递到左右子树上，该区间染色为0，然后根据更新区间的大小，在左右子树上去搜索。

求和的时候遇到区间的v>0的时候说明完全被染色过了，就把区间的长度乘以颜色的值加到总和里面去，然后结束这个方向的递归查询，

源程序+部分注释：

#include<stdio.h>
#include<iostream>
using namespace std;
struct node{
	int a,b,v;
}s[400000];

int t[150000],ans;

void Build(int x,int y,int num){
	s[num].a=x;	
	s[num].b=y;
	s[num].v=1;
	if(x==y)
		return ;	
	else{
		Build(x,(x+y)/2,num+num);
		Build((x+y)/2+1,y,num+num+1);
	}
}

void modify(int x,int y,int num,int value){
	if(x==s[num].a&&s[num].b==y){
		s[num].v=value;
		return ;
	}
	if(s[num].v==value)
		return ;
	if(s[num].v>0){
		s[2*num].v=s[2*num+1].v=s[num].v;
		s[num].v=0;
              //值往下传递。0代表混合染色
	}
	if(y<=(s[num].a+s[num].b)/2){
		modify(x,y,num+num,value);
	}
	else if(x>(s[num].a+s[num].b)/2)
		modify(x,y,num+num+1,value);
	else{	int mid=(s[num].a+s[num].b)/2;
		modify(x,mid,num+num,value);
		modify(mid+1,y,num+num+1,value);
	}
		
}

int getsum(int x,int y,int num){
	if(s[num].v>0){
		ans+=(s[num].b-s[num].a+1)*s[num].v;
		return 0;
	}
	else{
		if(y<=(s[num].a+s[num].b)/2)
			getsum(x,y,num+num);
		else if(x>(s[num].a+s[num].b)/2)
			getsum(x,y,num+num+1);
		else{
			getsum(x,(s[num].a+s[num].b)/2,num+num);
			getsum((s[num].a+s[num].b)/2+1,y,num+num+1);
		}
	}

}

int main(){
	int cas,n,k,i,v;
	int x,y,count;
	cin>>cas;
	k=1;
	while(cas--){
		ans=0;
		cin>>n;
		for(i=1;i<=n;i++){
			t[i]=1;
		}
		Build(1,n,1);
		scanf("%d",&count);
		for(i=1;i<=count;i++){
			scanf("%d %d %d",&x,&y,&v);
			modify(x,y,1,v);
		}
		getsum(1,n,1);
		printf("Case %d: The total value of the hook is %d.\n",k++,ans);
	}
	return 0;
}

hdu 1754(I HATE IT)

题目分析：学生ID编号分别从1编到N。
第二行包含N个整数，代表这N个学生的初始成绩，其中第i个数代表ID为i的学生的成绩。
接下来有M行。每一行有一个字符 C (只取'Q'或'U') ，和两个正整数A，B。
当C为'Q'的时候，表示这是一条询问操作，它询问ID从A到B(包括A,B)的学生当中，成绩最高的是多少。
当C为'U'的时候，表示这是一条更新操作，要求把ID为A的学生的成绩更改为B。

有一次参加农大月赛，因为对线段树的求区间最值的更新还是不熟练，所以出错了！缅怀！

#include<stdio.h>
int Max(int a,int b)
{
    return a>b?a:b;
}
struct node{
	int max,a,b;
}s[800000];

int t[200010];

void Build(int x,int y,int num){
	s[num].a=x;	s[num].b=y;
	if(x==y){
		s[num].max=t[x];
		return ;
	}
	else{
		Build(x,(x+y)/2,num+num);
		Build(((x+y)/2)+1,y,num+num+1);
		s[num].max=Max(s[num+num].max,s[num+num+1].max);
	}
}
int Query_max(int x,int y,int idx)
{
    if(x<=s[idx].a && s[idx].b<=y)
    {
        return s[idx].max;
    }
    if(y<=s[idx*2].b) return Query_max(x,y,idx*2);
    else if(x>=s[idx*2+1].a) return Query_max(x,y,idx*2+1);
    else return Max(Query_max(x,s[idx*2].b,idx*2),Query_max(s[idx*2+1].a,y,idx*2+1));
}
int modify(int x,int y,int num){
	if(s[num].a==x&&s[num].b==x){
		s[num].max=y;	
		return 0;
	}
	else{
		if(x<=s[num+num].b)
			modify(x,y,num+num);
		else 
			modify(x,y,num+num+1);
		s[num].max=Max(s[num+num].max,s[num+num+1].max);
	}
}

int main(){
	int n,cas,i,x,y;
	char c;
	while(scanf("%d %d",&n,&cas)!=EOF){
		for(i=1;i<=n;i++)
			scanf("%d",&t[i]);
		Build(1,n,1);
		while(cas--){
			getchar();
			scanf("%c %d %d",&c,&x,&y);
			if(c=='Q'){
				printf("%d\n",Query_max(x,y,1));		
			}
			else {
				modify(x,y,1);
			}
		}
		
	}
	return 0;
}

« 上一页 1 2 3 4 5 6 7 8 9 10 下一页 »