HDU (2855 Fibonacci Check-up)
题目大意:
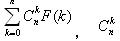 这个是组合数,然后求给定N,P让你求
这个是组合数,然后求给定N,P让你求![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) mod p的值是多少
mod p的值是多少
题目分析:
第一种方法:这里我引用一种常见的母函数:
(a+1)^n=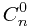 +
+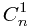 *a^1+
*a^1+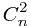 *a^2+....+
*a^2+....+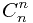 *a^n;
*a^n;
这里我可以知道fibonacci数可以用mitrax=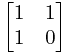 的乘积表示,f[i]=mitrax^i;
的乘积表示,f[i]=mitrax^i;
这里我们的“1”可以用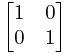 表示 即单位矩阵,这样我们只要求两个矩阵的的 i 次幂就可以了,这就直接转换到矩阵的二分法求快速幂上来了!注意一点,最后输出的[1][2]这个位置的数,别输出错了!
表示 即单位矩阵,这样我们只要求两个矩阵的的 i 次幂就可以了,这就直接转换到矩阵的二分法求快速幂上来了!注意一点,最后输出的[1][2]这个位置的数,别输出错了!
第二种方法:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) 最后证明结论等于:
最后证明结论等于:![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) = F[ 2* N ]
= F[ 2* N ]
引进fibonacci数的计算方程:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) ={
={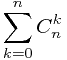 *(
*(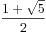 )^k -(
)^k -(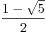 )^k}
)^k}
因为:
(a+1)^n=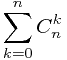 *a^k;
*a^k;
所以将上式化简成:
![$$\sum_{k=0}^{n}{C_n^k}{f[k]}$$ $$\sum_{k=0}^{n}{C_n^k}{f[k]}$$](/user_files/xuyemin520/epics/44f232ccb26e95b71fedea0811c888c3e173dbc3.png) =(
=(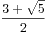 )^n+(
)^n+(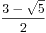 )^n
)^n
分子分母都乘*2 =(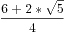 )^n+(
)^n+(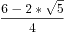 )^n
)^n
=(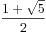 )^2n+(
)^2n+(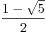 )^2n
)^2n
=F[ 2*N ]
我的代码是第一种的:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M {
int s[3][3];
};
int p;
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M b=paw(a,t/2);
if(t&1){
return multiply(multiply(b,b),a);
}
else
return multiply(b,b);
}
}
int main(){
struct M a,b;
int n,cas;
a.s[1][1]=2; a.s[1][2]=1;
a.s[2][1]=1; a.s[2][2]=1;
/*b.s[1][1]=1; b.s[1][2]=0;
b.s[2][1]=0; b.s[2][2]=1;*/
scanf("%d",&cas);
while(cas--){
scanf("%d %d",&n,&p);
if(n==0)
{ printf("0\n"); continue; }
b=paw(a,n);
printf("%d\n",b.s[1][2]);
}
return 0;
}
文章总结:(a+1)^n=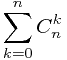 *a^k;这个母函数很好用 下次记得灵活运用!
*a^k;这个母函数很好用 下次记得灵活运用!
HDU 3117( Fibonacci Numbers 十大经典之二 :矩阵快速幂的应用)
题目大意:求
Fibonacci Numbers如果位数低于8位,则全部输出,否则只输出
前4位与后4位(注意后四位的0别忘记了,不过是什么格式,哪怕
0000都要输出);
题目分析:这里我们上一篇文章以前具体阐述了:
给定矩阵A,请快速计算出A^n(n个A相乘)的结果,输出的每个数都mod p。
由 于矩阵乘法具有结合律,因此A^4 = A * A * A * A = (A*A) * (A*A) = A^2 * A^2。我们可以得到这样的结论:当n为偶数时,A^n = A^(n/2) * A^(n/2);当n为奇数时,A^n = A^(n/2) * A^(n/2) * A (其中n/2取整)。这就告诉我们,计算A^n也可以使用二分快速求幂的方法。例如,为了算出A^25的值,我们只需要递归地计算出A^12、A^6、 A^3的值即可。根据这里的一些结果,我们可以在计算过程中不断取模,避免高精度运算。
然后我们以前有一篇文章已经阐述了,如果利用取对数求第N个fibonacci数的前4位有效数字;如果不清楚的话 请看我以前的一篇文章
“HDU 1568(非常经典微妙的 斐波纳契计算)“
代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
int sim[50]={0};
double f=(1+sqrt(5.0))/2;
double ff=(1-sqrt(5.0))/2;
struct M{
int s[5][5];
};
int solve_f4(int n){
double t=(-0.5)*log(5.0)/log(10.0)+(double(n))*log(f)/log(10.0);
double k=t-floor(t);
t=pow(10.0,k);
while(t<1000)
t*=10.0;
return (int)t;
}
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%10000)%10000;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M k=paw(a,t/2);
if(t&1){
return multiply(multiply(k,k),a);
}
else
return multiply(k,k);
}
}
int main(){
int n,k1,k2;
struct M a,b;
a.s[1][1]=1;
a.s[1][2]=0;
a.s[2][1]=0;
a.s[2][2]=1;
b.s[1][1]=b.s[1][2]=b.s[2][1]=1;
b.s[2][2]=0;
sim[0]=0;
sim[1]=1; sim[2]=1; sim[3]=2;
for(int i=4;i<=49;i++)
sim[i]=sim[i-2]+sim[i-1];
while(scanf("%d",&n)!=EOF){
if(n<=39){
printf("%d\n",sim[n]);
continue;
//其实我最初是用公式求前39个fibonacci数的
//但是发现有误差,所以改用数组直接模拟出来
}
else{
k1=solve_f4(n);
struct M k=paw(b,n-1);
k=multiply(k,a);
k2=k.s[1][1]%10000;
printf("%d...%04d\n",k1,k2);
}
}
return 0;
}
”
POJ 3070(Fibonacci )
题目分析:
经典题目6 给定n和p,求第n个Fibonacci数mod p的值,n不超过2^31
根 据前面的一些思路,现在我们需要构造一个2 x 2的矩阵,使得它乘以(a,b)得到的结果是(b,a+b)。每多乘一次这个矩阵,这两个数就会多迭代一次。那么,我们把这个2 x 2的矩阵自乘n次,再乘以(0,1)就可以得到第n个Fibonacci数了。不用多想,这个2 x 2的矩阵很容易构造出来:
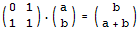
但是我这里稍微有点区别的是,我是构造: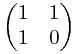 其实这里
其实这里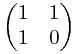 *
*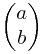 =
=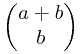
为了计算直观我把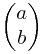 写成
写成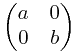 都一样的 其实 呵呵
都一样的 其实 呵呵
这里我们的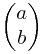 =
=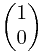
然后我们用二分的方法求矩阵的快速幂!
这里建议大家用结构体传递矩阵 这样很好用的!
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
struct M{
int s[5][5];
};
int p=10000;
struct M multiply(struct M a,struct M b){
struct M c;
memset(c.s,0,sizeof(c.s));
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
c.s[i][j]=(c.s[i][j]+ (a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
if(t==1)
return a;
else{
struct M c=paw(a,t/2);
if(t&1){
return multiply(c,multiply(c,a));
}
else{
return multiply(c,c);
}
}
}
int main(){
int n;
struct M a,d;
a.s[1][1]=a.s[1][2]=a.s[2][1]=1;
a.s[2][2]=0;
d.s[1][1]=1;
d.s[1][2]=0;
d.s[2][1]=0;
d.s[2][2]=1;
while(scanf("%d",&n),n!=-1){
if(n==0){
printf("0\n");
continue;
}
if(n==1||n==2){
printf("1\n");
continue;
}
struct M k=paw(a,n-1);
struct M b=multiply(d,k);
printf("%d\n",b.s[1][1]);
}
}
POJ 3233( 3233 Matrix Power Series 矩阵的快速幂 )
题目分析:
S = A + A2 + A3 + … + Ak.
求 S mod p;
我们要二分考虑
二分求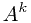 mod p
mod p
首先把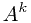 转化成:
转化成:
1) 如果k是偶数 (  mod p ) * (
mod p ) * (  mod p )这样就把就达到了降幂的作用
mod p )这样就把就达到了降幂的作用
2)如果k是奇数 (  mod p ) * (
mod p ) * (  mod p )* ( A mod p)
mod p )* ( A mod p)
然后再对求和的过程进行二分!
如果K是偶数我们把公式转换成 S=A + A2 + A3 + … +  +
+ *(A + A2 + A3 + … +
*(A + A2 + A3 + … +  )
)
如果K是奇数 则可以写成: S=A + A2 + A3 + … + 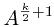 +
+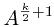 *(A + A2 + A3 + … +
*(A + A2 + A3 + … +  )
)
代码+部分注释:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
struct M{
int s[32][32];
};
int n,p;
struct M add(struct M a,struct M b){
int i,j;
struct M c;
memset(c.s,0,sizeof(c.s));
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
c.s[i][j]=(a.s[i][j]+b.s[i][j])%p;
return c;
}
struct M multiply(struct M a,struct M b){
int i,j,k;
struct M c;
memset(c.s,0,sizeof(c.s));
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
for(k=1;k<=n;k++)
c.s[i][j]=(c.s[i][j]+(a.s[i][k]*b.s[k][j])%p)%p;
return c;
}
struct M paw(struct M a,int t){
struct M b;
memset(b.s,0,sizeof(b.s));
if(t==0){
for(int i=1;i<=n;i++)
b.s[i][i]=1;
return b;
}
else{
struct M k=paw(a,t/2);
if(t&1){
return multiply(multiply(k,k),a);
}
else
return multiply(k,k);
}
}
struct M sum(struct M a,int t){
if(t==1){
return a;
}
else{
struct M tempt=sum(a,t/2);
if(t&1){
struct M k=paw(a,t/2+1);
return add(add(tempt,k),multiply(tempt,k));
}
else{
return add(tempt,multiply(tempt,paw(a,t/2)));
}
}
}
int main(){
int k,i,j;
struct M a;
cin>>n>>k>>p;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++){
scanf("%d",&a.s[i][j]);
a.s[i][j]%=p;
}
struct M tempt=sum(a,k);
for(i=1;i<=n;i++){
for(j=1;j<n;j++){
cout<<tempt.s[i][j]<<" ";
}
printf("%d\n",tempt.s[i][j]);
}
return 0;
}
HDU (2045 不容易系列之(3)—— LELE的RPG难题)
题目大意:有排成一行的n个方格,用红(Red)、粉(Pink)、绿(Green)三色涂每个格子,每格涂一色,要求任何相邻的方格不能同色,且首尾两格也不同色.求全部的满足要求的涂法.
题目分析:
这个题目刚刚开始,规律是找出来了,但是边界木有考虑好啊!
首先来分析一下:
假设求N个格子有多少种图法:
1)当N-1个与第一个相同颜色,所以这种图法不合法,从而映射出,第N-2个肯定合法!所以这时候我们有两种图法,即不用考虑第N-1个,只用考虑N-2合法的染法种类数 : 2*F[ N-2];
2) 当N-1个与第一个不相同,说明从第一个到第N-1个都是合法的图法,我们就不用考虑太多,这里只能用一种颜色了,您想啊,头用了一种颜色,N-1用了一种颜色,第N个既不能与第一个相同,又不能与第N-1个相同,那么只有一种颜色了,这时候只用考虑N-1的长度的合法种类: F[ n-1]
F[ N ] = F[ N-1 ]+2* F [ N-2 ];
但是这里要考虑边界问题!
f[1]=3;
f[2]=6;
f[3]=6;
这里的三个格子比较特殊,因为总公才3种颜色,相邻,头尾颜色各异,所以个数为2的 与格子数为3的 图法一样
代码:
#include<iostream>
#include<cstdio>
using namespace std;
double s[55]={0};
int main(){
int i,n;
s[1]=3;
s[2]=6;
s[3]=6;
for(i=4;i<=50;i++)
s[i]=s[i-2]*2+s[i-1];
while(scanf("%d",&n)!=EOF){
printf("%.0lf\n",s[n]);
}
return 0;
}
HDU (超级楼梯)
题目大意:
画个图也许您就明白了,如果您再加上一个台阶,图中就会多出两条线,一个是从n-2那里引来的,一条是从n-1那里引来的,所以F[N]=F[N-1]+F[N-2]
想必 猜出来了这是什么了吧 呵呵
这就是典型的feibonacci数
公式:
f[n]=
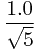 {
{ 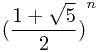 -
- 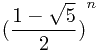 }
}但是这里直接模拟求解就可以了
代码:
#include<iostream>
#include<cstdio>
using namespace std;
long long s[45];
int main(){
int i,n,cas;
s[1]=1;
s[2]=1;
for(i=3;i<=40;i++)
s[i]=s[i-1]+s[i-2];
cin>>cas;
while(cas--){
scanf("%d",&n);
printf("%lld\n",s[n]);
}
return 0;
}
HDU 1134( Game of Connections Catalan数的第三种应用!)
给定N*2个点,求分别将其两两相连,每个点仅链接一次,而且每条线段不相交!
题目分析:
这又是Catalan数
直接套公式吧,其实证明目前我还没会,嘎嘎
公式:
f[n]=![$$\sum_{k=0}^{n-1}{{f[n-1-k]*f[k]}}$$ $$\sum_{k=0}^{n-1}{{f[n-1-k]*f[k]}}$$](/user_files/xuyemin520/epics/48603051e990bdfa0e8630541c65bd12c17861db.png) ;
;
直接计算就可以了,这里设计到大数的运算,我是用JAVA写的,不想用C模拟了 呵呵
代码:
import java.io.*;
import java.util.*;
import java.math.*;
public class Main {
public static void main(String args[]){
List list=new ArrayList(102);
BigInteger f=BigInteger.valueOf(1);
list.add(f);
list.add(f);
f=BigInteger.valueOf(2);
list.add(f);
for(int i=3;i<=100;i++){
BigInteger sum=BigInteger.valueOf(0);
for(int j=0;j<i;j++){
sum=sum.add( ((BigInteger)list.get(i-1-j)).multiply( ((BigInteger) list.get(j) )) );
}
list.add(sum);
}
Scanner cin=new Scanner(System.in);
int n;
while(cin.hasNext()){
n=cin.nextInt();
if(n==-1)
break;
System.out.println(list.get(n));
}
}
}
HDU 1131(Count the Trees)Catalan求树的构造方法数
题目大意:上面有一篇关于二叉树的构造方法数,这里只是普通的树,所以不用考虑次序。
Catalan数可以表示二叉树的构造方法数,Catalan数=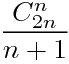 但是在这里我们不需要考虑次序,所以我们要乘以A(N,N);也就是N种元素的排列方法 也就是N!
但是在这里我们不需要考虑次序,所以我们要乘以A(N,N);也就是N种元素的排列方法 也就是N!
所以这里的方法数=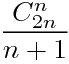 *A(N,N);
*A(N,N);
化简一下:
(n+2)*(n+3)*(n+4)*...*(2*n)
但是我这里直接把各个部分直接求出来的 嘿嘿,因为用JAVA写方便呀 所以都无所谓的啦
代码:
import java.io.*;
import java.util.Scanner;
import java.math.BigInteger;
public class Main{
public static BigInteger C(int n,int m){
BigInteger sum=BigInteger.valueOf(1);
for(int i=n;i>n-m;i--)
sum=sum.multiply(BigInteger.valueOf(i));
for(int j=1;j<=m;j++)
sum=sum.divide(BigInteger.valueOf(j));
return sum;
}
public static BigInteger jie(int n){
BigInteger sum=BigInteger.valueOf(1);
for(int i=1;i<=n;i++)
sum=sum.multiply(BigInteger.valueOf(i));
return sum;
}
public static void main(String args[]){
int n;
Scanner cin=new Scanner(System.in);
while(cin.hasNext()){
n=cin.nextInt();
if(n==0)
break;
BigInteger t1=C(2*n,n);
BigInteger t2=jie(n);
t1=t1.divide(BigInteger.valueOf(n+1));
t1=t1.multiply(t2);
System.out.println(t1);
}
}
}
HDU 1133(Buy the Ticket Catalan 数的另一种应用,非常重要!)
题目大意:M+N个人排队买票,票的单价是50¥,每个人只能买一张。 M个人拿50的去买,N个人拿100的去买,然后悲剧的是售票处开始的时候没有钱,所以如果拿100块买票人前面的拿50块买票的人小于或者等于用100块买票的人,这种排队方式就不合法,也就是不能顺利全部都买到票(因为没零钱找了)!
题目分析:
这是一个Catalan数的非常经典的应用,买票问题,首先我们用"0"表示用50块买票的人,用“1”表示用100块买票的人,然而假设m=4,n=3,的一个序列是:0110100显然,它不合法,然后我们把他稍微变化一下:把第一个不合法的“1”后面的所有数0位为1, 1位为0;这样我们得到了另一个序列:0111011,显然他也不是合法的,但是在这里我们关注的不是他合不合法!只是说明每个不合法的都有一个这样的序列跟他一一对应!
所以我们计算公式就是:合法的排列方式=所有排列方式-非法排列方式
我们这里非法排列方式的计算 就是:(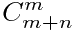 -
- 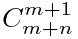 )*M!*N!,然而在这题,因为每个人都是不同的,所以还要乘以 M!*N!
)*M!*N!,然而在这题,因为每个人都是不同的,所以还要乘以 M!*N!
所以得出最终方程:
F(N)=(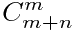 -
-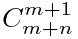 )*M!*N! ;
)*M!*N! ;
然后再化简一下;
F(N)=(M+N)! * (M-N+1)/(M+1)
大数运算模拟,
分别有:
大数阶乘
大数乘小数
大数除小数。
#include<iostream>
#include<cstdio>
#include<cstring>
#define MAX 201
using namespace std;
int factor[205][MAX]={0};
int sim[201]={0};
int multiply(int s[],int Max,int b){//the static number can't be a canliang
int ans=0,i;
for(i=Max;i>=1;i--){
ans+=s[i]*b;
s[i]=ans%10000;
ans=ans/10000;
}
return 0;
}
int div(int s[],int Max,int b){
int ans=0,t,i;
for(i=1;i<=Max;i++){
t=ans*10000+s[i];
s[i]=t/b;
ans=t%b;
}
return 0;
}
int getfactor(){
int i;
factor[0][MAX-1]=factor[1][MAX-1]=1;
for(i=2;i<=203;i++){
memcpy(factor[i],factor[i-1],MAX*sizeof(int));//this has a falut that i have replace memcpy by strcpy!
multiply(factor[i],MAX-1,i);
}
return 0;
}
int output(int *s,int k){
int i=1;
printf("Test #%d:\n",k);
while(s[i]==0&&i<MAX)
i++;
printf("%d",s[i++]);
for(;i<MAX;i++)
printf("%04d",s[i]);
printf("\n");
return 0;
}
int main(){
int m,n,i,k=1;
getfactor();
while(scanf("%d %d",&m,&n),m+n){
memcpy(sim,factor[m+n],sizeof(int)*MAX);
/*for(i=1;i<=MAX;i++){
for(int j=1;j<MAX;j++)
cout<<factor[i][j];
cout<<endl;
}*/
if(n>m){
printf("Test #%d:\n",k++);
printf("0\n");
//别忘记了 判断这种情况,
//当初为了这个BUG找了好苦,5555....
continue;
}
multiply(sim,MAX-1,m-n+1);
div(sim,MAX-1,m+1);
output(sim,k);
k++;
}
return 0;
}
HDU 1130(Catalan数的应用)
题目大意:就是给你1到N个数,让你求他能构成多少种二叉树;
题目分析:这里又是一种组合数学里的重要知识点!Catalan数的应用。
如果数据比较小,建议模拟这个公式:
Catalan的原始递推公式就是这个,这个是专门针对给出节点,有多少二叉数构造方法的方程。
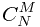 =
=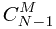 +
+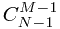
用二维数组模拟,当前元素的值等于他正上方的值+左边的值;
当然所消耗的内存是很大的 :M*N*4 Bytes,所以数字小才能模拟50以内比较保险 哈哈{^_^}!
然后大数的就只有应用到大数的算法啦,反正我认为C++里的模拟太费事了 ,所以今天第一次也学习写
JAVA里的大数的运算了, 建议您也学学,嘿嘿,方便啊 。
首先分析一下思路:
这个方程进一步化简:
F( N )=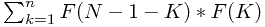 (k=0....N-1)
(k=0....N-1)
根据这个公式进行计算就可以了
import java.math.*;
import java.util.*;
public class Main{
public static void main(String args[]){
List list=new ArrayList(101);
BigInteger f=BigInteger.valueOf(1);
list.add(f);
list.add(f);
for(int i=2;i<=100;i++){
f=BigInteger.valueOf(0);
for(int j=0;j<i;j++)
f=f.add(((BigInteger)list.get(j)).multiply( (BigInteger)list.get(i-1-j)));
list.add(f);
}
Scanner cin=new Scanner(System.in);
int inputInt=0;
while(cin.hasNext()){
inputInt=cin.nextInt();
System.out.println(list.get(inputInt));
}
}
}