HDU （1893 Sibonacci Numbers）
题目大意：
f(1)=1
f(2)=1
f(n)=f(n-1)+f(n-2) (n>=3)
Now Sempr found another Numbers, he named it "Sibonacci Numbers", the definition is below:
f(x)=0 (x<0)
f(x)=1 (0<=x<1)
f(x)=f(x-1)+f(x-3.14) (x>=1)
题目分析：
这个题目是黑书上的弱化版，黑书有对这一系列问题进行讨论，然后这里，你只需要把数放大100倍，这样只要递归求解就可以了，注意要用字符串里出来输入的数据哦，因为我们最多只需要小数点后的2位，后面都舍去‘
代码：
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long s[100100];
int init(){
int i;
for(i=0;i<=100;i++)
s[i]=1;
for(i=100;i<=100100;i++){
if(i<314)
s[i]=s[i-100]%1000000007;
else
s[i]=(s[i-100]+s[i-314])%1000000007;
}
return 0;
}
int main(){
int cas,n,i;
char ch[20];
init();
scanf("%d",&cas);
while(cas--){
scanf("%s",ch);
if(ch[0]=='-'){
printf("0\n");
continue;
}
i=0;
n=0;
int len=strlen(ch);
while(ch[i]!='.'&&i<len)
n=n*10+ch[i++]-'0';
if(i+1<len)
n=n*10+ch[i+1]-'0';
else
n=n*10;
if(i+2<len)
n=n*10+ch[i+2]-'0';
else
n=n*10;
printf("%lld\n",s[n]);
}
return 0;
}
HDU 1892（See you~ 简单二维树状数组）
题目大意：
S x1 y1 x2 y2 means you should tell me the total books of the rectangle used (x1,y1)-(x2,y2) as the diagonal, including the two points.
A x1 y1 n1 means I put n1 books on the position (x1,y1)
D x1 y1 n1 means I move away n1 books on the position (x1,y1), if less than n1 books at that position, move away all of them.
M x1 y1 x2 y2 n1 means you move n1 books from (x1,y1) to (x2,y2), if less than n1 books at that position, move away all of them.
就这几个操作
题目分析：
这题唯一注意的地方是给出的点不一定是前面的比后面的小，我是说查询以这两点为对角线的矩形里面的书的数量的时候，还有你要更新到1001，因为你为防止0的死循环，所以把每个坐标，都加1 这样可以防止死循环；如果他输入 是（1000 ，1000） ，你要计算的是(1001,1001) 所以你要更新到1001！
#include<iostream>
#include<cstdio>
#include<cstring>
#define lowbit(x) (x&(-x))
using namespace std;
int s[1005][1005],num[1005][1005];
int getsum(int x,int y){
int t,sum;
sum=0;
while(x>0){
t=y;
while(t>0){
sum+=s[x][t];
t-=lowbit(t);
}
x-=lowbit(x);
}
return sum;
}
void modify(int x,int y,int count){
int t;
while(x<=1001){
t=y;
while(t<=1001){
s[x][t]+=count;
t+=lowbit(t);
}
x+=lowbit(x);
}
return ;
}
int main(){
int cas,times,i,j,k;
int x1,x2,y1,y2,n;
int maxx,maxy,minx,miny;
char ch[10];
scanf("%d",&cas);
for(k=1;k<=cas;k++){
printf("Case %d:\n",k);
for(i=1;i<=1002;i++)
for(j=1;j<=1002;j++){
num[i][j]=1;
s[i][j]=lowbit(i)*lowbit(j);
}
scanf("%d",×);
while(times--){
scanf("%s",ch);
if(ch[0]=='S'){
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
x1++; y1++; x2++; y2++;
maxx=x1>x2?x1:x2;
maxy=y1>y2?y1:y2;
minx=x1<x2?x1:x2;
miny=y1<y2?y1:y2;
x2=maxx; x1=minx;
y2=maxy; y1=miny;
int ans=getsum(x2,y2)-getsum(x1-1,y2)-getsum(x2,y1-1)+getsum(x1-1,y1-1);
printf("%d\n",ans);
}
if(ch[0]=='A'){
scanf("%d %d %d",&x1,&y1,&n);
x1++; y1++;
num[x1][y1]+=n;
modify(x1,y1,n);
}
if(ch[0]=='D'){
scanf("%d %d %d",&x1,&y1,&n);
x1++; y1++;
if(num[x1][y1]<=n){
n=num[x1][y1];
}
num[x1][y1]-=n;
n=-n;
modify(x1,y1,n);
}
if(ch[0]=='M'){
scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2,&n);
x1++; y1++; x2++; y2++;
if(num[x1][y1]<=n){
n=num[x1][y1];
}
num[x1][y1]-=n;
num[x2][y2]+=n;
modify(x1,y1,-n);
modify(x2,y2,n);
}
}
}
return 0;
}
BNUOJ 4359 无爱的编号（一个不错的DP ）
题目大意：http://gnu.bnu.edu.cn/contest/problem_show.php?pid=4359
Description
众所周知，拉手网有许多客户，由于客户数量实在过于庞大，因此拉手网希望为每位客户进行编号以便更好的为客户服务。每个编号为一个由 ‘0’~‘9’组成的N位数字。考虑到很多人不喜欢数字4和数字13，因此我们称包含4或包含13的编号为无爱编号，如134、84、121351都是无 爱编号，123则不是无爱编号。现在我们希望知道，所有N位的编号中，刨除掉无爱编号后剩余的编号数量。这个编号数量可能很大，我们只要知道结果的最后8 位即可。
Input
输入的第一行是一个整数T，表示数据组数。
Output
对于每组数据，输出一个8位整数表示编号数量的最后8位。若编号数量不足8位则用前导零填充。
题目分析： 唉，比赛的时候一个劲的往组合数学方面写，最后郁闷死掉了 ，用组合数学写，貌似太难了 ，至少我不会，没写出来，后来看了解题报告，终于 终于。。。恍然大悟 。原来是一道简单的 dp， 由于对dp 不是很敏感，所以当时没相当 状态转移方程，汗颜呐
看看题目吧：
这里我们用dp[i][0] 表示 前 i 位不包含 4与 13的编号数目 且最后一位不是1 ， dp[i][1] 表示 前 i 位不包含4 与 13的 编号数目，但最后一位是1！
然后我们得到方程：
dp[i][0] = 8*dp[i-1][0]+7*dp[i-1][1] // 前 i -1位 合法的但最后位不为1的编号后面可以填 8个数字，（除去 1与4 因为4是
非 法的 、dp[i][0]最后位不能为1,） ,前i-1 位合法，但最后一位是1的， 我们只能
在其后面填 其他7个数字 得到新的合法编号（除去1 ，3， 4）
dp[i][1]=dp[i-1][0] + dp[i-1][1]; // 这里在第i位 填1 不会构成不合法编号，所以只要把前面 i-1位的所有情况加起来就可以
可以了
最后一步只要
total[i]=dp[i][0]+dp[i][1] 就是我们要求的总的方案数，
代码：
#include<iostream>
#include<cstdio>
using namespace std;
int num[1000100][2];
int main(){
num[0][0]=1;
num[0][1]=0;
for(int i=1;i<=1000000;i++){
num[i][0]=(8*num[i-1][0]+7*num[i-1][1])%100000000;
num[i][1]=(num[i-1][0]+num[i-1][1])%100000000;
}
int cas,n,ans;
scanf("%d",&cas);
while(cas--){
scanf("%d",&n);
printf("%08d\n",(num[n][0]+num[n][1])%100000000);
}
return 0;
}
POJ（1061 青蛙的约会 扩展欧几里德求解不定方程）
题目大意：
Description
我们把这两只青蛙分别叫做青蛙A和青蛙B，并且规定纬度线上东经0度处为原点，由东往西为正方向，单位长度1米，这样我们就得到了一条首尾相接的 数轴。设青蛙A的出发点坐标是x，青蛙B的出发点坐标是y。青蛙A一次能跳m米，青蛙B一次能跳n米，两只青蛙跳一次所花费的时间相同。纬度线总长L米。 现在要你求出它们跳了几次以后才会碰面。
Input
会很大的！所以只能 用 扩展的欧几里德 求这个不定方程！
第一步里面 化简后的标准方程的一组解麽？然后我已经求得 标准方程的一组解了，继续讨论 解系里面的最小值吧！
#include<iostream>
#include<cmath>
#include<cstdio>
using namespace std;
long long gcd(long long a,long long b){
long long c;
if(a<b){
c=a; a=b;
b=c;
}
while(b){
c=b;
b=a%b;
a=c;
}
return a;
}
long long extended_gcd(long long a,long long b,long long &x,long long &y){
long long ans,t;
if(b==0){
x=1; y=0;
return a;
}
else{
ans=extended_gcd(b,a%b,x,y);
t=x; x=y;
y=t-(a/b)*y;
}
return ans;
}
int main(){
long long x,y,m,n,l;
long long a,b,d,k,s,t;
while(scanf("%lld %lld %lld %lld %lld",&x,&y,&m,&n,&l)!=EOF){
a=n-m;
b=l;
d=x-y;
long long r=gcd(a,b);
if(d%r!=0){
printf("Impossible\n");
continue;
}
a/=r;
b/=r;
d/=r;
extended_gcd(a,b,s,k);
s=s*d;
k=k*d;
t=s/b;
s=s-t*b;
if(s<0)
s+=b;
printf("%lld\n",s);
}
return 0;
}
hit2813 Garden visiting 关于组合数的一个简单的拆分求解
题目大意：给你n * k 的矩形，始点在矩形的左上角，出口在矩形的右下角，求出最快走出这个矩阵的，方案数。
题目分析：最短的走出矩阵的方案的路程肯定是N+k，然后我们把这个路程离散化成N+K个状态，但是每种走法，的起点，跟终点的状态都一样的，只不过N+K-2里面有不同的走法， 我们换位思考一下，在N+K-2个状态里有有K-1个状态 分别投影在 K边的不同的点上面，因为，你必须往下移动K-1个单位才能到达出口，所以在竖直方向上必须有K-1个状态分别投影在K边的不同点上，这样我们就得出了方案数的组合数，就是在N+K-2里面选k-1个！公式：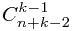 
计算方面就是把这个组合数分别分解成素数，然后对素数进行求解，取模！
代码+部分注释：
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int pri[20000],num[20000],cnt,p;
bool flag[200001];
void get_pri(){
memset(flag,true,sizeof(flag));
int i,j;
pri[1]=2;
cnt=1;
for(i=4;i<=200000;i+=2)
flag[i]=false;
for(i=3;i<=3000;i+=2)
for(j=i*i;j<=200000;j+=2*i)
flag[j]=false;
for(i=3;i<=200000;i+=2)
if(flag[i])
pri[++cnt]=i;
return ;
}
int paw(int a,int t){
int ans=1;
while(t){
if(t%2==1)
ans=(ans*a)%p;
a=(a*a)%p;
t/=2;
}
return ans;
}
int solve(){
int cas,n,k,c,s,i;
long long ans;
scanf("%d",&cas);
while(cas--){
scanf("%d %d %d",&k,&n,&p);
if(k>n){
c=k; k=n;
n=c;
}
n=k+n-2;
k--;
if(k==n){
printf("%d\n",1%p);
continue;
}
for(i=1;i<=n&&pri[i]<=n;i++)
num[i]=0;
for(i=1;pri[i]<=n&&i<=cnt;i++){
s=pri[i];
while(n>=s){
num[i]+=n/s-(n-k)/s-k/s;
s*=pri[i];
}
}
ans=1;
for(i=1;i<=cnt&&pri[i]<=n;i++){
if(num[i]>0)
ans=(ans*paw(pri[i],num[i]))%p;
if(ans==0)
break;
}
printf("%lld\n",ans);
}
return 0;
}
int main(){
get_pri();
solve();
return 0;
}
FOJ（1753 Another Easy Problem 又一种整数分解）
题目大意：就是给你多个组合数，让你求出
C(n1,m1)==0 (mod M)
C(n2,m2)==0 (mod M)
C(n3,m3)==0 (mod M)
的最大的M满足上式，
题目分析：
其实就是把这些组合数，分解成素数因子，然后求每个因子出现的最少的次数，题目不难 但时间卡的好紧，我超时得想吐，如果您也遇到跟我一样的情况，请你细细看我 代码提示的各个优化环节！不懂的 留言，我们一起讨论
代码+部分注释：
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int pri[1000011];
bool flag[1000001];
int sim[1000001];
int num1[151],num2[151];
int cnt;
void get_pri(){//生成素数表
for(int i=1;i<=1000000;i++)
flag[i]=true;
pri[1]=2;
cnt=1;
flag[0]=flag[1]=false;
for(int i=4;i<=1000000;i+=2)
flag[i]=false;
for(int i=3;i<3000;i+=2)
for(int j=i*i;j<=1000000;j+=2*i)
flag[j]=false;
for(int i=3;i<=1000000;i+=2)
if(flag[i])
pri[++cnt]=i;
return ;
}
int paw(int a,int t){
int ans=1;
while(t){
if(t%2==1)
ans=ans*a;
a=a*a;
t/=2;
}
return ans;
}
void solve(){
int cas,n,k,i,s,j,t;
bool flag;
int maxn;
while(scanf("%d",&cas)!=EOF){
flag=false;
maxn=0;
for(i=1;i<=cas;i++){
scanf("%d %d",&num1[i],&num2[i]);
if(maxn<num1[i])
maxn=num1[i];
if(num1[i]==num2[i])
flag=true;
//如果哦值为1的情况，就不用计算了，肯定就是1啦！
}
if(flag){
printf("1\n");
continue;
}
for(j=0;j<=100000;j++)
sim[j]=2147483647;
for(t=0;t<cas;t++){
n=num1[t+1];
k=num2[t+1];
for(i=1;i<=cnt&&pri[i]<=maxn;i++){
if(sim[i]==0)//这也是一个优化的地方，如果是0，
//这个素数在各个组合数里出现的最少次数肯定是0啦
continue;
int sum=0;
int p=pri[i];
while(n>=p){//这个就是计算各个素数在组合数里出现的次数
sum=sum+n/p-k/p-(n-k)/p;
p*=pri[i];
//记得一次把这个写错了写成“p*=p”悲剧哦，段错误，肯定超出int范围啦！
}
if(sum<sim[i])
sim[i]=sum;
//sim[i]是记录第i个素数在各个组合数里出现的最少的素数！
}
}
long long ans=1;
//下面这个循环就无非是 计算每个组合数里，各个素数出现的最少次数，
//组合成的数ans，也就是题目要求的数！
for(i=1;i<=cnt&&pri[i]<=maxn;i++){
if(sim[i]>0&&sim[i]!=2147483647){
ans=ans*paw(pri[i],sim[i]);
}
}
printf("%lld\n",ans);
}
return ;
}
int main(){
get_pri();
solve();
return 0;
}
PKU （2992 Divisors 整数分解的经典应用！）
题目大意：就是给你一个组合数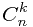
这里0=<k=<n=<341
题目分析：
1.约数个数定理：
设n的标准质因数分解为n=p1^a1*p2^a2*...*pm^am,
则n的因数个数=(a1+1)*(a2+1)*...*(am+1).
2. 对于任意质数p，n！中有（n/p+n/p^2+n/p^3+...)个质因子p。
代码+部分注释：
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int pri[200];
bool flag[532];
int cnt;
void get_pri(){
for(int i=1;i<=431;i++)
flag[i]=true;
pri[1]=2;
cnt=1;
flag[0]=flag[1]=false;
for(int i=4;i<=431;i+=2)
flag[i]=false;
for(int i=3;i<23;i+=2)
for(int j=i*i;j<=431;j+=2*i)
flag[j]=false;
for(int i=3;i<=431;i+=2)
if(flag[i])
pri[++cnt]=i;
return ;
}
int main(){
int n,k,s,i;
int num[100];
get_pri();
while(scanf("%d %d",&n,&k)!=EOF){
memset(num,0,sizeof(num));
for(i=1;i<=cnt;i++){
s=n;
if(s<pri[i])
break;
while(s){
num[i]+=s/pri[i];
s/=pri[i];
}
}
for(i=1;i<=cnt;i++){
s=n-k;
if(s<pri[i])
break;
while(s){
num[i]-=s/pri[i];
s/=pri[i];
}
}
for(i=1;i<=cnt;i++){
s=k;
if(s<pri[i])
break;
while(s){
num[i]-=s/pri[i];
s/=pri[i];
}
}
long long sum=1;
for(i=1;i<=cnt;i++)
if(num[i]>0)
sum*=num[i]+1;
printf("%lld\n",s);
}
return 0;
}
POJ （1811 Prime Test 关于miller_rabin的素数判断和pollard_rho的整数分解）
题目大意：就是给一个很大的数，让你判断是否为素数，如果不是则计算出小于等于他的最小的素数。2 <= N < 254
题目分析： 这里由于数字非常大，我们不能按照常规思路来做，
miller_rabin的素数判断：Fermat小定理：若n为素数，则,有an-1≡1(mod n)，大部分的都满足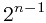
=1(mod n)，但是这不能包含所有情况，所以我们利用随机函数，来随机产生在2～n-2直接的数进行测试，如果没测出来，几乎就可以判断这个数是素数，这样做n太大了，计算起来肯定会超时的，要知道n的范围：2～2^54 这样太可怕了，这样的话我们来优化：
首先n-1= m*2q ，2^(n-1)=(2^m)^2q 在这里求m,与q应该是非常简单的事情吧，然后我们怎么办呢？这里我可以利用随机数a枚举
(2^m)^2q （q=1..q-1），因为这些式子是 2^(n-1)的因数，如果他们不是素数，那么证明N不是素数，反之是素数（只是说概率很大可以 看作是了），
这里还有一种情况，就是该数不是素数，然后就要分解整数，求出最小的一个素数，这里分解整数，用到的是pollard_rho分解法：
这里证明我就不写了，水平有限，只写过程：
首先我们用随机函数生成一个x1（1<x1<n）,然后根据x1 构造出x2 ( f[x]=x1^2+c )然后 这里假设有p 能够整除 x1-x2 ，x1-x2=p*q,这里q显然可以整除x1-x2，但是x1-x2不能整除n，从而可以得到，q不能整除 n，所以gcd( (x1-x2) ,n )有可能得到1，也有可能得到n的一个因数，所以我们进行随机枚举，这样就可以计算出n的因数分解形式。
代码+部分注释：
#include<iostream>
#include<cstdio>
#include<ctime>
#include<cstdlib>
using namespace std;
long long top=0,pri[100];
long long multiply( long long a,long long b,long long n){
long long exp,res=0;
//这个就是用加法，来模拟乘法，为了防止运算的数太大，
exp=a%n;
while(b){
if(b&1){
res+=exp;
if(res>n)
res-=n;
}
exp<<=1;
if(exp>n)
exp-=n;
b/=2;
}
return res;
}
long long paw(long long a,long long t,long long n){
long long ans=1;
a=a%n;
while(t){
if(t%2==1)
ans=multiply(ans,a,n);
a=multiply(a,a,n);
t/=2;
}
return ans;
}
long long gcd(long long a,long long b){
long long c;
if(a<b){
c=a;
a=b; b=c;
}
while(b){
c=b;
b=a%b;
a=c;
}
return a;
}
bool miller_rabin(long long n,long long ti){
if(n==2)
return true;
if(n<2||!(n&1))
return false;
long long p=n-1;
long long k=0,a,x;
while(p%2==0){
p/=2;
k++;
}
long long ans;
srand(time(0));
for(int t=1;t<=ti;t++){
a=rand()%(n-1)+1;
x=paw(a,p,n);
for(int i=1;i<=k;i++){
ans=multiply(x,x,n);
if(ans==1&&x!=1&&x!=n-1)
return false;
x=ans;
}
if(ans!=1)
//注意这个判断！
return false;
}
return true;
}
long long pollard_rho(long long a,long long k,long long n){
srand(time(0));
long long x=rand()%(n-1)+1;
long long i=1,t=2;
long long y=x;
while(1){
i++;
x=(multiply(x,x,n)+k)%n;
long long ans=gcd(y-x,n);
if(ans>1&&ans<n)
return ans;
if(x==y)
return n;
if(t==i){
y=x;
t*=2;
}
}
}
void search(long long n,long long k){
if(miller_rabin(n,10)){
pri[++top]=n;
return ;
}
else{
long long p=n;
while(p>=n)
p=pollard_rho(p,k--,n);
search(p,k);
search(n/p,k);
}
}
int main(){
int cas,i;
long long n;
cin>>cas;
while(cas--){
scanf("%lld",&n);
if(miller_rabin(n,10ll))
printf("Prime\n");
else{
top=0;
search(n,180);
long long min=-1;
for(i=1;i<=top;i++){
if(min<0||min>pri[i])
min=pri[i];
}
printf("%lld\n",min);
}
}
return 0;
}
ZOJ（2562 More Divisors 求反素数经典应用！）
题目大意：给一个N求不超过N的 哪个数的因子数最多，数目相同的取值小的那个！
题目分析：这里引进反素数知识：
反素数第一点：g(x)表示 x含有因子的数目，设 0<i<=x 则g(i)<=x;
反素数第二个特性：2^t1*3^t2^5^t3*7^t4..... 这里有 t1>=t2>=t3>=t4...
所以我们根据这两个属性 进行递归求解！
递归过程：
首先做出三条判断，第一是否该值不超过N的大小，第二比较因子的个数，更新最大的，即更新最大的反素数，第三如果因子数相等，则更新较小的。
然后枚举+递归不断尝试更新，使得得到因子数最大的那个！
代码+部分注释：
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long bestres,bestsum,n;
long long pri[16]={2,3,5,7,11,13,17,19,23,29,31,37,41,43,47};
//res表示当前讨论的值，sum表示该值的因子数目，
//k表示讨论到第几个素数了，limit表示上次的幂的值
//这次幂的上限，就是体现t1>=t2>=t3...
void work(long long res, long long sum,int k,int limit ){
if(res>n)//如果超过n就跳出！
return ;
if(sum>bestsum){
//这次计算的因子数目比我以前过程的最大值还大，那么就要更新！
bestres=res;
bestsum=sum;
}
if(sum==bestsum&&res<bestres){
//如果因子数目一样，取值比较小的！
bestres=res;
}
long long p=pri[k];
//记得第一次p=pri[k],因为下面i是从1开始计数的！
for(int i=1;i<=limit;i++,p*=pri[k]){
if(res*p>n)
break;
else
work(res*p,sum*(i+1),k+1,i);
}
}
int main(){
while(scanf("%lld",&n)!=EOF){
bestres=1LL;
bestsum=1LL;
work(1LL,1LL,0,50);
printf("%lld\n",bestres);
}
return 0;
}
POJ（2689 Prime Distance经典的区间筛选素数！）
题目大意：给出一个区间，长度<=1000 000；求其中素数相邻素数之间的差最小的和最大的（左右端点的最值可以为2147483647）；
题目分析：这里因为左右端点的数值过大，所以没办法用常规方法操作！ 但是这里 区间的长度才1000000 这样的长度操作难度还是可以接受的 不会超时。
在这里我们先求出能表示2147483647的质因子 其实这个范围不大 就是sqrt(2147483647) 50000以内！ 这里我着重解释一下为什么需要求2147483647？ 举个例子说明，让你求一个区间a,b里相邻素数的最小、最大差值。
这里我们分两种情况讨论：
第一种：就是小数类型的a,b（也就是说b不大于2147483647里的最大质因子）
这里我们只需要枚举，比较过去就可以了，不是吗？
第二种:a,b非常之大！ 超过了2147483647里的最大质因数的值，这里我们该怎么办呢？
你会怎么做？第一我也跟你一样 ，真不知道如何转换， 您别灰心， 其实这里我们用到就是区间平移。何为区间平移？：就是把在长度为1000000的数组里进行模拟，下标为0的位置上的值 表示a的状态（就是指他是不是素数,"false"代表不是，反之则是素数！），下标为i上的值 表示 a+i 是否为素数！
然后要怎么做呢？ 这里其实想通了 就好理解了，任何数都能用素数表示，对吗？如果这个数 不是任何比他小的素数的倍数（这里1没算素数），那么他肯定是素数，有木有？这样的话就好办了，我们只要把用来模拟平移的区间里，所有是2147483647的质因子的倍数全部筛选掉不就行了么？这里还补充一点 为什么是2147483647里面的质因子呢？因为你a,b肯定是比2147483647小，对吧？他的质因子肯定能够包含你的，所以用他的进行筛选，才是完整的满足任何一个在2147483647里面的大数。
这里我格外对代码和注意的地方强调一下！：
第一：for(i=1;i<=k;i++){
start=l/pri[i]*pri[i];
if(start<l)
start+=pri[i];
start-=l;
for(j=start;j<=end;j+=pri[i])
res[j]=false;
}// l 是（L）的小写形式
这是什么意思呢？start=l/pri[i]*pri[i]
就是求出最接近l的 start 能够整除pri[i]的数
例如 l=5；pri[i]=3；
start=l/pri[i]*pri[i] 之后start=3；
如果 start<l
那么start+=pri[i]
这里start=6了
6是不是最接近5 并且能够整除3 的呢？
懂了吗 ？如果不懂 您就留言吧
还有 一个注意的地方：
这里1不是素数，所以当输入的数第一个为1的时候 要自行加上一个1！不然就是错误的！
代码+注释：
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
bool flag[1000001]={0};
int ans[1000001];
int pri[50000];
bool res[1000001];
int k;
void init(){
int i;
k=1;
pri[1]=2;
for(i=4;i<=50000;i+=2)
flag[i]=1;
for(i=3;i<=50000;i+=2){
if(!flag[i]){
pri[++k]=i;
for(int j=2*i;j<=5000;j+=i)
flag[j]=1;
}
}
return ;
}
void solve(){
int i,j,times;
long sn1,en1,dis,mind,maxn,l,u,sn2,en2;
long start,end;
while(scanf("%ld %ld",&l,&u)!=EOF){
end=u-l;
if(l==1)
l++;
if(u<pri[k]){
times=0;
for(i=l;i<=u;i++)
if(!flag[i])
ans[++times]=i;
}
else{
for(j=0;j<=end;j++)
res[j]=true;
for(j=(l%2!=0);j<=end;j+=2)
res[j]=false;
for(i=1;i<=k;i++){
start=l/pri[i]*pri[i];
if(start<l)
start+=pri[i];
start-=l;
for(j=start;j<=end;j+=pri[i])
res[j]=false;
}
times=0;
for(i=0;i<=end;i++)
if(res[i])
ans[++times]=i+l;
//这里记得复原 移动的区//间哦题目要求的是区间，所以您得记得复原区间哦
}
mind=2147483647;
maxn=0;
for(i=1;i<times;i++){
if(mind>ans[i+1]-ans[i]){
sn1=ans[i];
en1=ans[i+1];
mind=ans[i+1]-ans[i];
}
if(maxn<ans[i+1]-ans[i]){
sn2=ans[i];
en2=ans[i+1];
maxn=ans[i+1]-ans[i];
}
}
if(maxn==0){
printf("There are no adjacent primes.\n");
continue;
}
printf("%ld,%ld are closest, %ld,%ld are most distant.\n",sn1,en1,sn2,en2);
}
}
int main(){
init();
solve();
return 0;
}